Разработка нелинейного радиолокатора для обнаружения электронных устройств, содержащих нелинейные компоненты, страница 17

Для анализа особенностей режима колебаний 2-го рода выполним гармонический анализ тока стока.

Воспользуемся основным уравнением транзистора:

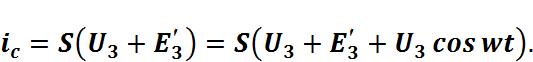  (2.8.1.3)

С целью получения удобного для анализа выражения произведем следующие преобразования.

В соответствии с Рис. 2.8.1.4. при wt = Q, i_c = Q, поэтому

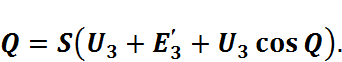  (2.8.1.4)

Вычитая из (2.8.1.3) уравнение (2.8.1.4) получим

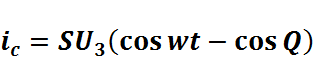   .    (2.8.1.5)

Далее при wt = 0, i_c = I_max.

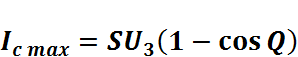Тогда   .  (2.8.1.6)

Разделим уравнение (2.8.1.5) на (2.8.1.6) и решим относительно i_c. Получим

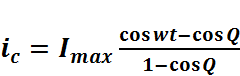   .    (2.8.1.7)

Угол отсечки  определим из уравнения (3.7)

    

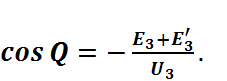
В полученном выражении смещение E₃ и потенциал затирания транзистора  необходимо подставлять с учетом знака.

С целью гармоничного анализа разложим выражение для  формула (2.8.1.7) в ряд Фурье

 

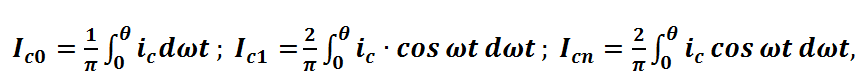
где I_c0 – постоянная составляющая тока ; I_cn – амплитуды переменных составляющих, где n = 1,2,3…

Введем понятие коэффициента разложения (коэффициенты Берга)

   

Оптимальный угол отсечки для получения максимальной амплитуды n-й гармоники вычисляется по формуле   

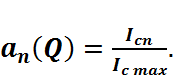
Рис. 2.8.1.5. Зависимость коэффициентов Берга от угла отсечки. Зависимость коэффициентов Берга от угла отсечки представлены на Рис. 2.8.1.5. Рассмотрим энергетические отношения в режиме колебаний 2-го рода. –полезная мощность в нагрузке;  – потребляемая мощность от источника. Коэффициент полезного действия: .  (2.8.1.8) В формуле (2.8.1.8)соотношения, входящие в нее, будут иметь значения:  ; .

Как видим, коэффициент полезного действия в режиме колебаний 2-го рода значительно больше такового в режиме колебаний 1-го рода.

В этом большая выгода использования такого режима в генераторах.

2.8.2. Особенности  СВЧ преселекторов приемника.

К основным особенностям построения преселекторов приемников на СВЧ относится трудность достижения требуемых номиналов L и C элементов в сосредоточенном исполнении при приемлемой добротности, возрастающая значимость паразитных параметров сосредоточенных элементов и частотные свойства активных элементов.

Для решения задачи построения пассивных фильтровых и согласующих цепей СВЧ существует множество методов. Однако по совокупности свойств в настоящее время преобладает метод реализации цепей на основе несимметричных полосковых линий с твердым диэлектриком (НПЛТД).

НПЛТД представляет собой линию, в которой проводник ленточного, круглого или квадрат­ного сечения расположен на некотором расстоянии от металлической плоскости (основания), а пространст­во между проводником и основаниями за­полнено диэлектриком (Рис. 2.8.2.1).

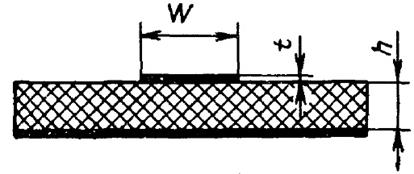
Рис. 2.8.2.1. Несимметричная полосковая линия с твердым диэлектриком.

Такая линия являет­ся простой в настройке, изготовлении и эксплуатации. Однако к ее недостаткам относятся невысокий уровень экранировки электромагнитного поля и значительные потери (порядка 3 дБ/мачмитуельные ень экранировки электромагнитного поля и обротности, возрастающая значимость множества паразитных парметров сосре). Если относительная диэлектрическая проницаемость подложки , а ширина полоски  - линию называют микрополосковой. Микрополосковые линии часто используют в СВЧ ИМС.

Для справедливости расчетных соотношений и модельных представлений необходимо чтобы толщина проводника t и заземленной пластины составляли бы не менее 3…5 толщины скин-слоя, а ширина заземленной пластины – не менее 3W. При проектировании схем на различных видах НПЛТД необходимо рассчитывать, чтобы рабочая частота была ниже критической:

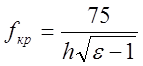 [ГГц],

где h – толщина диэлектрической подложки в мм.

Потери в НПЛТД складываются из потерь в проводнике р_с, потерь в диэлектрике р_d и потерь вследствие излучения р_i:

,

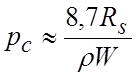 [дБ/м],  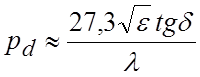[дБ/м], 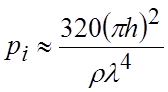 [дБ/м], где - сопротивление поверхностного проводящего слоя на центральной рабочей частоте [Ом/м²], ρ – волновое сопротивление линии,  - тангенс диэлектрических потерь, λ – длина волны в свободном пространстве для центральной рабочей частоты.