Разработка нелинейного радиолокатора для обнаружения электронных устройств, содержащих нелинейные компоненты, страница 23

соотношение (2.9.2.5) можно свести к следующему: 

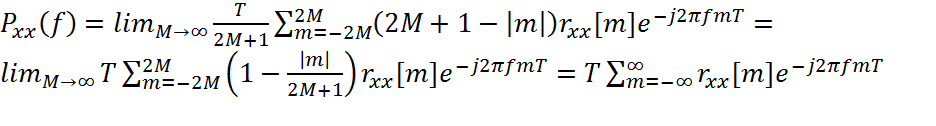 (2.9.2.6)

Заметим, что на последнем этапе вывода (2.9.2.6) использовалось допущение о том, что автокорреляционная последовательность "затухает", так что

.

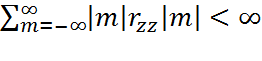 Взаимосвязь двух определений СПМ (2.9.2.1) и (2.9.2.4) наглядно показывает диаграмма, представленная на рисунке 2.9.2.1.
 Если в выражении (2.9.2.4) не учитывать операцию математического ожидания, то получим оценку СПМ

, 

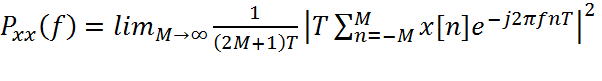которая называется выборочным спектром.

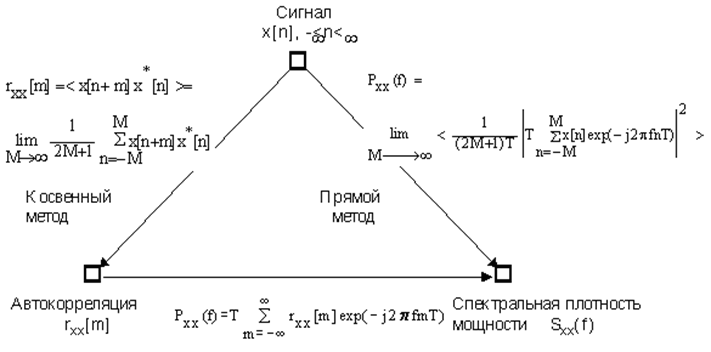
Рис. 2.9.2.1. Взаимосвязь двух способов оценивания спектральной плотности мощности.

Коррелограммный метод оценивания СПМ - это просто подстановка в выражение (2.9.3.1) конечной последовательности значений оценки автокорреляции (коррелограммы) вместо бесконечной последовательности неизвестных истинных значений автокорреляции[27].

2.9.3. Окна.

Один из важных вопросов, который является общим для всех классических методов спектрального оценивания, связан с взвешиванием данных. Обработка с помощью окна используется для управления эффектами, обусловленными наличием боковых лепестков в спектральных оценках. Заметим, что имеющуюся конечную запись данных удобно рассматривать как некоторую часть соответствующей бесконечной последовательности, видимую через применяемое окно. Так последовательность наблюдаемых данных x₀[n] из N отсчетов математически можно записать как произведение бесконечной последовательности x[n] и функции прямоугольного окна

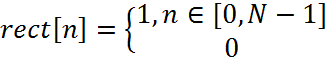
x₀[n]=x[n]·rect[n].

При этом принимается очевидное допущение о том, что все ненаблюдаемые отсчеты равны нулю независимо от того, так ли это на самом деле. Дискретно-временное преобразование Фурье взвешенной последовательности равно свертке преобразований последовательности x[n] и прямоугольного окна rect[n]

X₀(f)=X(f)*D_N(f) ,

где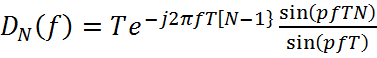  

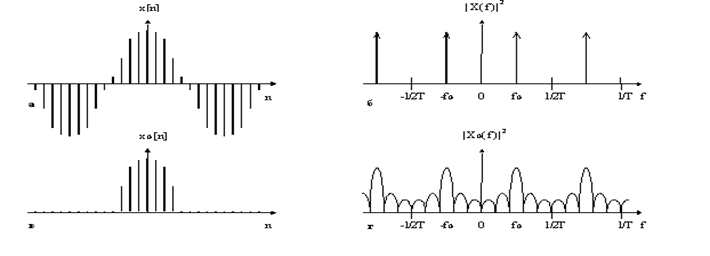Функция D_N(f), называемая дискретной функцией sinc, или ядром Дирихле, представляет собой ДВПФ прямоугольной функции. Преобразование наблюдаемой конечной последовательности является искаженной версией преобразования бесконечной последовательности. Влияние прямоугольного окна на дискретно-временную синусоиду с частотой f₀ иллюстрирует Рис. 2.9.3.1.

Рис. 2.9.3.1. Иллюстрация смещения дискретно-временного преобразования Фурье вследствие просачивания из-за взвешивания данных.: а, в - исходная и взвешенная последовательности; б, г - их преобразования Фурье.

Из рисунка видно, что острые спектральные пики ДВПФ бесконечной синусоидальной последовательности расширились за счет свертки с преобразованием окна. Таким образом, минимальная ширина спектральных пиков взвешенной окном последовательности определяется шириной главного лепестка преобразования этого окна и не зависит от данных. Боковые лепестки преобразования окна будут изменять амплитуды соседних спектральных пиков (иногда это явление называют просачиванием). Поскольку ДВПФ - периодическая функция, то наложение боковых лепестков от соседних периодов может привести к дополнительному смещению. Увеличение частоты отсчетов позволяет ослабить эффект наложения боковых лепестков. Аналогичные искажения будут, естественно, наблюдаться и в случае несинусоидальных сигналов. Просачивание приводит не только к появлению амплитудных ошибок в спектрах дискретных сигналов, но может также маскировать присутствие слабых сигналов. Можно предложить ряд других функций окна, применение которых позволяет снизить уровень боковых лепестков по сравнению с тем, который имеется при использовании прямоугольного окна. Снижение уровня боковых лепестков будет уменьшать смещение спектральной оценки, однако это дается ценой расширения главного лепестка спектра окна, что, естественно, приводит к ухудшению разрешения. Следовательно, и здесь должен выбираться какой-то компромисс между шириной главного лепестка и уровнем боковых лепестков. Для оценки качества окон используется несколько параметров. Традиционным показателем является ширина полосы главного лепестка на уровне половинной мощности. В качестве второго показателя используется эквивалентная ширина полосы, введенная выше. Два показателя используются и для оценки характеристик боковых лепестков. Первый - их максимальный уровень, второй - скорость спадания, характеризующая быстроту уменьшения боковых лепестков по мере удаления от главного лепестка.