Случайный процесс называется стационарным в широком смысле, если его среднее значение постоянно (не зависит от времени), а автокорреляция зависит только от разности индексов времени m=n1-n2 (временного сдвига или задержки между отсчетами). Таким образом, стационарный в широком смысле дискретный случайный процесс x[n] характеризуется постоянным средним значением <x>=<x[n]> и автокорреляционной последовательностью (АКП)
rxx[m] = < x[n+m]x*[n] >.
Отметим следующие свойства АКП:
rxx[0] ≥ |rxx[m]| , rxx[-m] = r*xx[m] ,
которые
справедливы при всех m.
Спектральная плотность мощности (СПМ) определяется как дискретно-временное
преобразование Фурье (ДВПФ) автокорреляционной последовательности
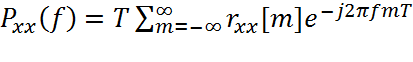 . (2.9.2.1)
. (2.9.2.1)
СПМ, ширина которой полагается ограниченной значениями ±1/2T Гц, является периодической функцией частоты с периодом 1/T Гц. Функция СПМ описывает распределение мощности случайного процесса по частоте. Для подтверждения избранного для нее названия рассмотрим обратное ДВПФ
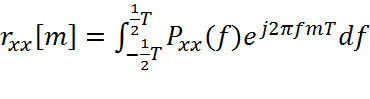 , (2.9.2.2)
, (2.9.2.2)
вычисляемое при m=0
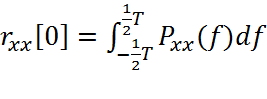 .
(2.9.2.3)
.
(2.9.2.3)
Автокорреляция при нулевом сдвиге характеризует среднюю мощность случайного процесса. Согласно (2.9.2.3), площадь под кривой Pxx(f) характеризует среднюю мощность, поэтому Pxx(f) представляет собой функцию плотности (мощность на единицу измерения частоты), которая характеризует распределение мощности по частоте. Пару преобразований (2.9.2.1) и (2.9.2.2) часто называют теоремой Винера-Хинчина для случая дискретного времени. Поскольку rxx[-m]=r*xx[m], то СПМ должна быть строго действительной положительной функцией. Если АКП - строго действительная функция, то rxx[-m]=rxx[m] и СПМ можно записать в форме косинус-преобразования Фурье
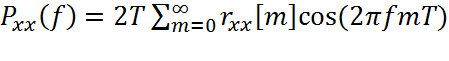 ,
,
что означает также, что Pxx(f) = Pxx(-f), т.е. СПМ - четная функция.
До сих пор мы при определении среднего значения, корреляции и спектральной плотности мощности случайного процесса пользовались статистическим усреднением по ансамблю. Однако на практике обычно не удается получить ансамбль реализаций требуемого процесса, по которому можно было бы вычислить эти статистические характеристики. Желательно оценивать все статистические свойства по одной выборочной реализации x(t), заменяя усреднение по ансамблю усреднением по времени. Свойство, позволяющее такую замену осуществить называется эргодичностью. Говорят, что случайный процесс эргодичен, если с вероятностью, равной единице, все его статистические характеристики можно предсказать по одной реализации из ансамбля с помощью усреднения по времени. Иными словами, средние значения по времени почти всех возможных реализаций процесса с вероятностью единица сходятся к одной и той же постоянной величине - среднему значению по ансамблю
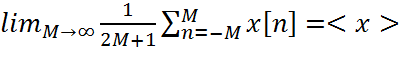 .
.
Этот предел, если он существует, сходится к истинному среднему значению тогда и только тогда, когда дисперсия среднего по времени стремится к нулю, что означает выполнение следующего условия:
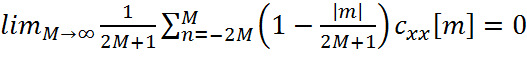 .
.
Здесь
cxx[m]
- истинное значение ковариации процесса x[n].
Аналогично, наблюдая значение произведения отсчетов процесса x[n]
в два момента времени, можно ожидать, что среднее значение будет равно
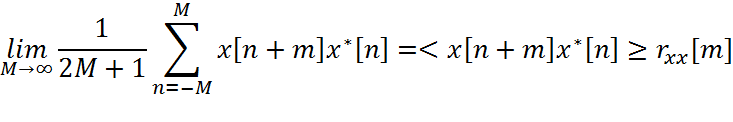
Допущение об эргодичности позволяет не только ввести через усреднение по времени определения для среднего значения и автокорреляции, но также дать подобное определение и для спектральной плотности мощности
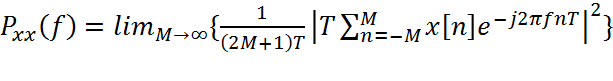 . (2.9.2.4)
. (2.9.2.4)
Эта эквивалентная форма СПМ получается посредством статистического усреднения модуля ДВПФ взвешенной совокупности данных, поделенного на длину записи данных, для случая, когда число отсчетов увеличивается до бесконечности. Статистическое усреднение необходимо здесь потому, что ДВПФ само является случайной величиной, изменяющейся для каждой реализации x[n]. Для того, чтобы показать, что (2.9.2.4) эквивалентно теореме Винера-Хинчина, представим квадрат модуля ДВПФ в виде произведения двух рядов и изменим порядок операций суммирования и статистического усреднения:
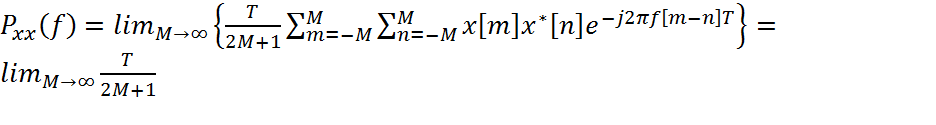
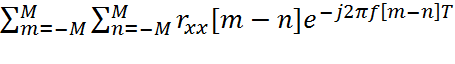 (2.9.2.5)
(2.9.2.5)
Используя известное выражение
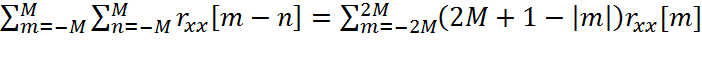 ,
,
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.