Разработка нелинейного радиолокатора для обнаружения электронных устройств, содержащих нелинейные компоненты, страница 18

В целях уменьшения габаритов полосковой линии, а также для подавления возникающих в ней высших типов волн стараются уменьшать ширину проводящей полоски, но уменьшение ши­рины полоски приводит к увеличению потерь. По этой же причине в случае НПЛТД трудно реализовать линию с большим волновым сопротивлением, так как с увели­чением волнового сопротивления ширина полосок стано­вится настолько малой, что резко возрастают потери в проводнике, а требования к допускам при их изготов­лении становятся трудно реализуемыми. Волновое сопротивление полосковой линии можно увеличить путем снижения ε, однако при этом возраста­ют потери линии на излучение. В тех случаях, когда потери на излучение несим­метричной линии оказыва­ются неприемлемо большими, при­меняют специальный экран, у которого верх­няя крышка расположена на расстоянии, значитель­но превышающем толщину подложки.

Наиболее востребованными в преселекторах приемников на СВЧ являются ФНЧ и полосовые фильтры.

Реализация ФНЧ. Наиболее простая и компактная реализация ФНЧ осуществляется путем использования чередующихся отрезков линии с низким волновым сопротивлением ρ_н и высо­ким волновым сопротивлением ρ_в при волновом сопро­тивлении подводящих линий ρ₀ (Рис. 2.8.2.2).

Рис. 2.8.2.2. Топология ФНЧ (вид сверху)

Топология ФНЧ может быть ориентировочно рассчитана по приведенным формулам и окончательно определена с помощью моделирования в МО. Говорить о приближенном расчете приходится не только потому, что для облегчения расчета формулы упрощены, но и потому, что поле окружающее НПЛТД частично находится в воздухе, а частично в диэлектрике подложки и геометрические размеры звеньев фильтра определяются эффективной относительной диэлектрической постоянной ε_эфф, которая сама зависит от этой геометрии.

Первоначально задаются граничная частота фильтра  по уровню a_п и частота начала полосы задержания  по уровню a_з, а также способ аппроксимации передаточной характеристики. Кроме того, необходимо задаться параметрами подложки (ε и h) и волновыми сопротивлениями ρ_н, ρ_в и ρ₀.

Определяем количество элементов фильтра:

- для аппроксимации по Чебышеву - ,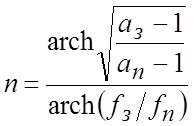

- для аппроксимации по Баттерворту - ,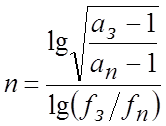

где параметр а представляет собой разы по мощности.

Чебышевский ФНЧ с нечетным чис­лом п элементов имеет одинаковые нагрузочные сопро­тивления слева и справа: ρ₀ = ρ_n+1.  Величина нагрузоч­ного сопротивления при четном числе п элементов в общем случае требует более детального рассмотрения. ФНЧ с аппроксимацией по Баттерворту при любом числе элементов имеет одинаковые нагрузочные сопротивления слева и справа.

Пользуясь справочной литературой для выбранных частот и количества элементов фильтра, находим обобщенные реактивные параметры элементов прототипа ФНЧ.

Преобразуем обобщенные реактивные параметры элементов ФНЧ:

,

,

где , L_i и C_i - индуктивности и емкости элементов, i=1…n.

Определяем ширину отрезков линии передачи  (j=1…3) для различных ρ_j из формулы:

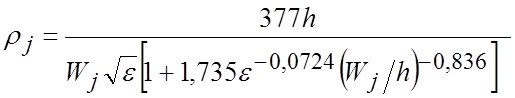                        [Ом].                          (I)

Вычисляем первое приближение для длины нечетного i-го отрезка линии передач фильтра :

,

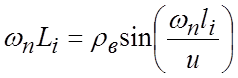где .

Вычисляем длины четных отрезков линий передачи фильтра, представляющих емкостные проводимости:

,

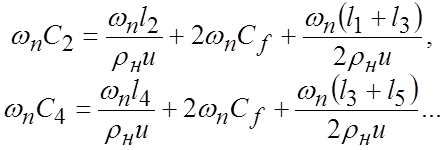где .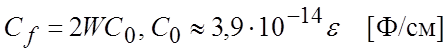

Уточняем длины нечетных отрезков, представляющих индуктивные сопротивления:

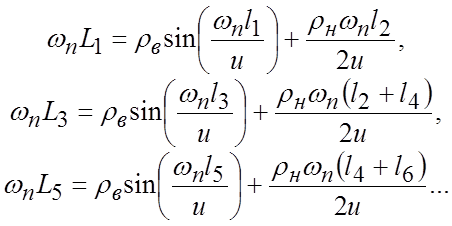
Полученные приближенные значения параметров топологии ФНЧ целесообразно подстраивать в соответствии с требованиями, используя среду МО.

Реализация полосовых фильтров. Наиболее простая и компактная реализация полосовых фильтров осуществляется использованием одинаковых связанных линий (Рис. 2.8.2.3).

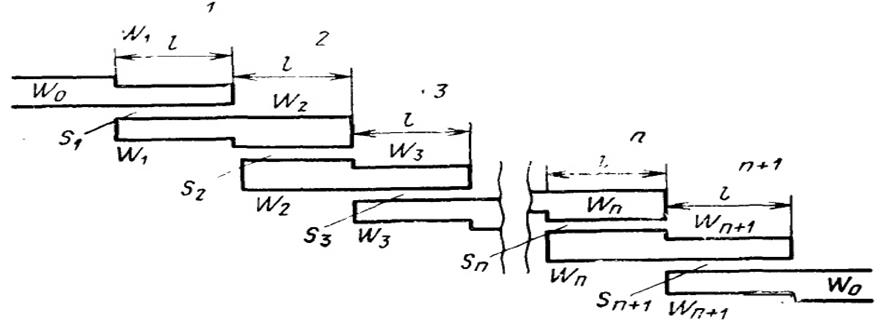
Рис. 2.8.2.3. Топология полосового фильтра (вид сверху).

Как правило, такие фильтры, выполненные на печатной плате, применяются в диапазоне частот 1…10 ГГц. При этом ширина полосы рабочих частот составляет 0,01…0,2 от центральной рабочей частоты f₀ для аппроксимации по Баттерворту, и 0,01…0,25 – по Чебышеву. Данные фильтры имеют паразитные полосы пропускания, расположенные вблизи частот кратных f₀.