Разработка нелинейного радиолокатора для обнаружения электронных устройств, содержащих нелинейные компоненты, страница 20

Физические основы: Поверхностные акустические волны были впервые описаны лордом Релеем в 1885. Распространяясь вдоль поверхости и проникая в глубину на расстояние 2-3 длины волны, именно этот тип волн является самым разрушительным при землетрясениях. Исследование ПАВ с целью применения для обработки радиосигналов начались в послевоенные годы, но вплоть до конца 70-х годов устройства на ПАВ использовались исключительно в военном оборудовании: радарах, космических системах связи. Высокая технологичность и стремительное развитие беспроводной телефонии в 80-е годы обеспечило этим устройствам широкое поле для применения в гражданских приложениях.

В простейшем применении трансверсальный фильтр на ПАВ состоит из двух преобразователей со встречными решетками проводящих электродов, расположенных на поверхности пьезоэлектрической подложки, например, монокристаллического кварца или ниобата лития (Рис. 2.8.3.1.).

Рис. 2.8.3.1. Трансверсальный фильтр на ПАВ.

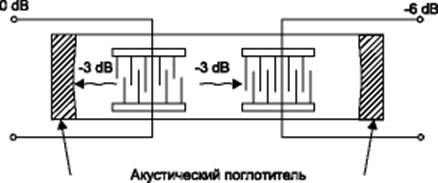
Один из этих преобразователей возбуждает, а другой принимает рэлеевскую волну. Если подать на передающий преобразователь сигнал в виде дельта-функции, то импульсный отклик фильтра будет являться сверткой локальных импульсных откликов двух преобразователей. Расстояние между соседними электродами составляет половину длины рэлеевской волны. Скорость таких волн на пять порядков меньше скорости света. Отсюда становится ясно, что на маленькой подложке можно воспроизвести сотни или тысячи периодов требуемого радиоимпульса.

Основы дизайна фильтров: Теперь предположим, что требуется создать фильтр с прямоугольной частотной характеристикой, как показано на Рис. 2.8.3.2.а.

Рис. 2.8.3.2. Основы дизайна фильтров.

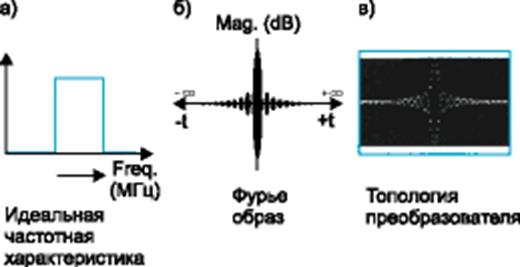
а) Идеальная частотная характеристика.

б) Образ Фурье.

в) Топология преобразования.

Импульсный отклик, соответствующий такой характеристике, показан на Рис. 2.8.3.2.б. Если воспроизвести топологию преобразователя в соответствии с этим импульсным откликом, то можно ожидать, что такой фильтр на центральной частоте, соответствующей периоду заполнения, будет иметь частотную характеристику, приближающуюся к заданной (Рис. 2.8.3.2.в). Конечно, для проектирования фильтров с малыми потерями и резонаторов используются более сложные методы.

2.9. Быстрое Преобразование Фурье (БПФ).

2.9.1. Основы БПФ.

Отображение спектрального разложения принятого сигнала на дисплее устройства может помочь в определении типа обнаруженной нелинейности. Так же возможно создание некой базы спектральных разложений различных нелинейных элементов, позволяющих более точно идентифицировать обнаруженный объект. Для получения спектрального разложения необходимо применить к принятому сигналу Быстрое преобразование Фурье (БПФ) – это название целого ряда эффективных алгоритмов, предназначенных для быстрого вычисления дискретно-временного ряда Фурье.  Основная проблема, возникающая при практической реализации ДВРФ, заключена в большом количестве вычислительных операций, пропорциональном N². Хотя еще задолго до появления компьютеров было предложено несколько эффективных вычислительных схем, позволяющих существенно сократить число вычислительных операций, настоящую революцию произвела публикация в 1965 году статьи Кули (Cooly) и Тьюки (Tukey) c практическим алгоритмом быстрого (число операций Nlog₂N) вычисления ДВРФ. После этого было разработано множество вариантов, усовершенствований и дополнений основной идеи, составивших класс алгоритмов, известных под названием быстрого преобразования Фурье. Основная идея БПФ - деление N-точечного ДВРФ на два и более ДВРФ меньшей длины, каждый из которых можно вычислить отдельно, а затем линейно просуммировать с остальными, с тем чтобы получить ДВРФ исходной N-точечной последовательности.
Представим дискретное преобразование Фурье (ДВРФ) в виде

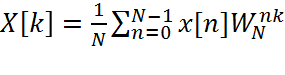, (2.9.1.1) 

где величина W_N= exp(-j2^π/N) носит название поворачивающего множителя (здесь и далее в этом разделе период выборки T равен 1). Выделим из последовательности x[n] элементы с четными и нечетными номерами