Теневой оптический метод каустик – метод исследований напряжений и деформаций, страница 9

Как правило, наиболее важным членом, расширяющим область применения решения первого порядка, является член второго порядка. Этот член характеризуется постоянным напряжением в направлении х (а_л = а2), которое добавляется к сингулярному распределению напряжений ближнего поля. Однако теневой оптический эффект чувствителен только к градиентам напряжений. Постоянные напряжения не создают изменений длины оптического пути [см. уравнения (9.1), (9.2) и (9.7)]. Та

ким образом, член второго порядка не оказывает какого-либо влияния на формирование каустики¹). При решении практических задач оптический метод каустик может иметь значительные преимущества перед другими оптическими методами (такими, как фотоупругость, муар или голографическая интерферо

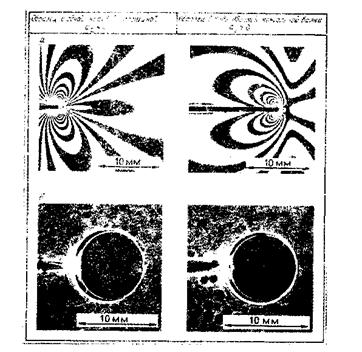
Рис. 9.21. Влияние члена второго порядка в уравнениях, характеризующих поле напряжений вблизи кончика трещины на картины полос фотоупругости (а) и теневых фигур-каустик (б).

метрия), с помощью которых непосредственно измеряются напряжения или деформации. Рис. 9.21 иллюстрирует влияние члена второго порядка на оптические теневые и фогоупругие картины, характеризующие распределение напряжений вблизи кончика трещины. Для образцов с одной краевой трещиной

¹⁾Это утверждение справедливо лишь для единичных каустик, получаемых на изотропных материалах. Однако некоторое влияние членов второго порядка может иметь место вследствие наличия члена, характеризующего анизотропию (А-т^О) в уравнении (9.7), когда образуются двойные каустики.

знак коэффициента а₂ отрицателен, что делает полосы-изохро-мы наклоненными вперед, тогда как для образцов в виде двойной консольной балки знак а₂ положителен, так что изохромы наклонены назад. Эти изменения в картинах изохром могут создать серьезные трудности при обработке картин полос вблизи кончика трещины. Однако теневые оптические картины одинаково независимы от знака коэффициента второго порядка

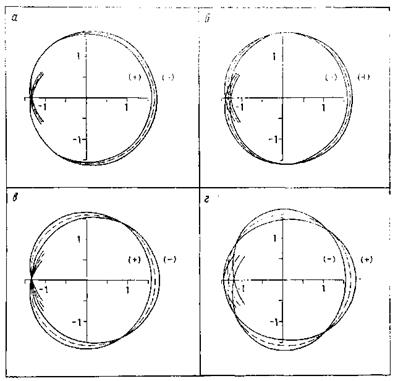
Рис. 9.22. Влияние на форму каустик членов высокого порядка, содержащих г^² (а), г (б), г³/² (в) и г² (г), в уравнениях, характеризующих поле напряжений вблизи кончика трещины.

Члены порядка выше второго оказывают влияние на формирование каустик. На рис. 9.22 показаны изменения формы каустик из-за наличия членов до четвертого порядка. Сравниваются формы каустик для произвольных величин отдельных коэффициентов и их разных знаков (т. е. для положительных и отрицательных коэффициентов) с формой каустик ближнего поля. Поскольку на практике коэффициенты при членах более

высокого порядка неизвестны, количественная оценка влияния членов высокого порядка на форму каустик затруднена. В практических приложениях целесообразно сравнивать форму экспериментально получаемых каустик с теоретической формой каустики для ближнего поля. Заметные изменения формы каустик свидетельствуют о влиянии членов более высокого порядка. Однако следует поступать осторожно при оценке величин коэффициентов интенсивности напряжений с помощью таких каустик.

Каустики при упруго-пластических деформациях,

Для трещин в пластичных материалах (таких, как конструкционные стали) линейная теория упругости несправедлива. Поле напряжений вблизи кончика трещины описывается здесь соотношениями теории пластичности. Величина напряжений ограничивается пределом текучести, и, следовательно, деформации вблизи кончика трещины становятся неограниченными. Таким образом, вместо задачи об упругой концентрации напряжений возникает задача о концентрации пластических деформаций. Однако, как и в случае упругой концентрации напряжений, каустики характеризуют пластическую концентрацию деформации [6, 7].

Применительно к стальным образцам, изучаемым по схеме отражения, справедлив следующий подход. При деформации поверхности образца изменение длины оптического пути в соответствии с уравнением (9.3) составляет

где а — общая толщина образца. Уменьшение толщины образца вследствие пластическойдеформации е равно