Теневой оптический метод каустик – метод исследований напряжений и деформаций, страница 7

Теневой оптический эффект от перемещения wиз плоскости не имеет места при просвечивании, так как поверхности пластины хотя и искривляются, но остаются параллельными. Следовательно, лучи света, пересекающие пластину, не отклоняются, а лишь слегка смещаются.

Поэтому уравнения проецирования для трех типов нагружения трещин имеют следующий вид:

а)  тип I:

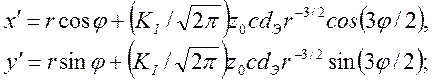
б)  тип II:

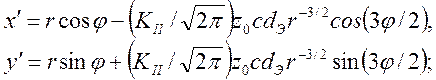                                  (2.18)

в)  тип III:

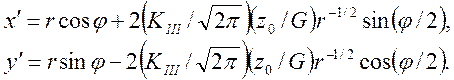
Для простоты здесь рассматривается лишь изотропный случай. С применением уравнения (2.10) получаем следующие уравнения начальных кривых:

а)  тип I:

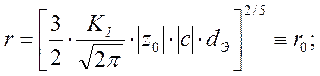
б)  тип II:

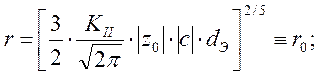                                                     (2.19)

в)  тип III:

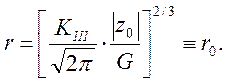
Как и в рассмотренных выше примерах, начальные кривые представляют собой окружности постоянного радиуса г₀ с центром в начале координат.

С помощью уравнений проецирования (2.18) получаем следующие уравнения каустик как изображений начальных кривых уравнений (2.19):

а)  тип I:

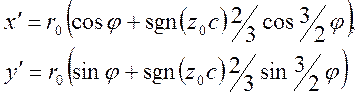
б)  тип II:

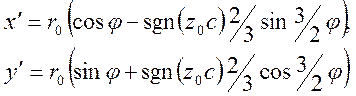,                                                          (2.20)

в)  тип III:

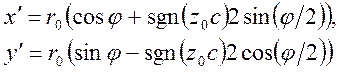
Форма каустик для трех типов нагружения трещин и различных возможных видов наблюдения показана на рис. 13. В противоположность каустикам при нагружснии типа I, форма каустик при нагружснии типов II и III ассиметрична. Графическое изображение распределения лучей света для теневых картин трещин при нагружениях типов II и III показано па рис. 14. Распределение света в случае трещины при нагружениях типа I показано на рис. 9.

Нетрудно убедиться, что характерный размер Dкаустик на рис. 13 связан с радиусом начальных кривых соотношениями:

(тип I),      (тип II),    (тип III).                 (2.21)

Рис. 13. Форма каустик вблизи кончика трещины при нагружениях типов I, II и III. Р – положительная нагрузка; N –-отрицательная нагрузка; RI – действительное изображение; VI – мнимое изображение; ТА – схема просвечивания; RА (или RЕ) —схема отражения.

Рис. 14. Схемы образования теневых оптических картин трещин при нагруженных типов II (a) и III (б) в случае отражения.

Следовательно, с учетом формул (2.19) и (2.21) получаем следующие зависимости дли трех типов нагружения:

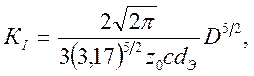
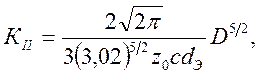                                                                           (2.22)

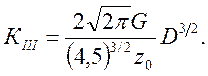
Результаты для трещин при смешении типов нагружения I и II получаем суперпозицией уравнений, описывающих поля напряжений, и, следовательно, уравнении проецирования лучей света для случаен I п II. Форма каустик для различных значений отношения коэффициентов интенсивности напряжений  показана на рис. 15, а. В зависимости от величины отношения  возможны все промежуточные формы каустик от типа I до типа II.

С помощью двух размеров каустик D_max и D_min, показанных на рис. 15, б, можно определить коэффициенты интенсивности напряжений K_Iи K_II. Па рис. 16 с помощью уравнений (2.20) для каустик смешанного типа построена зависимость измеренной величины  от отношения . С помощью графика па рис. 17 определяется величина коэффициента g, описывающего связь между диаметром каустики D_max и радиусом начальной кривой r₀. Таким образом, абсолютную величину K_I можно вычислить с использованием измеренной величины D_max по формуле

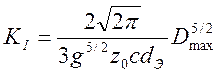                                                                                  (2.23)

Рис. 15. Форма каустик для трещин при смешанных типах нагружения (а) и определение величин Dmax и Dmin (б).

Рис. 16. Изменение размеров каустики в зависимости от отношения μ при смешанном тиле нагружения.	Рис. 17. Изменение коэффициента gв зависимости от величины отношения μ коэффициентов интенсивности напряжений при смешанном нагружении.

Динамические каустики

Рассматриваются два типа динамических задач механики разрушения: стационарные трещины при динамическом нагружснии и движущиеся трещины при стационарной внешней нагрузке.