Изменение длины оптического пути ΔS происходит из-за изменения толщины пластины и показателя преломления материала. Для пластины с плоскими параллельными поверхностями получаем
![]() (2.3)
(2.3)
где s – длина оптического пути; dэ – эффективная толщина пластины; п – показатель преломления и dэ=dдля прозрачных образцов; п=-1 и dэ= d/2 для непрозрачных образцов при отражении; d– действительная толщина образца.
|
|
|
Рис. 5. Схема отклонения лучей света. |
При просвечивании на изменение длины оптического пути лучей света влияют деформации поверхности с двух сторон образца и изменение показателя преломления по всей толщине образца. При отражении изменение длины оптического пути определяется только деформацией передней освещенной поверхности образца (рис. 6). Таким образом, случай отражения получается из более общего случая просвечивания, если формально положить n=-1 (что соответствует изменению направления лучей света и Δn=0) и принять эффективную толщину dэ=d/2 (поскольку рассматривается деформация только одной поверхности).
Изменения показателя преломления Δn от действия главных напряжений σ1, σ2, σ3 описываются законом Максвелла – Неймана. Для общего случая двоякопреломляющего прозрачного материала
![]() (2.4)
(2.4)
где Aи В – константы материала. Для оптически изотропных недвоякопреломляющих материалов A=Bи Δn1=Δn2=Δn. При отражении А=В=0. Изменения Δdэ под действием напряжений характеризуются законом Гука:
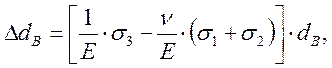 (2.5)
(2.5)
где ![]() в случае плоского напряженного состояния, ΔdЭ=0 при плоской деформации,
Е – модуль упругости, ν – коэффициент Пуассона. С помощью выражений
(2.4) и (2.5) уравнение (2.3) преобразуем к виду:
в случае плоского напряженного состояния, ΔdЭ=0 при плоской деформации,
Е – модуль упругости, ν – коэффициент Пуассона. С помощью выражений
(2.4) и (2.5) уравнение (2.3) преобразуем к виду:
![]() (2.6)
(2.6)
где ![]() и
и ![]() для
плоского напряженного состояния;
для
плоского напряженного состояния; ![]() и
и ![]() для плоской деформации. Уравнения (2.6)
могут быть записаны в более удобном виде через сумму и разность главных
напряжений:
для плоской деформации. Уравнения (2.6)
могут быть записаны в более удобном виде через сумму и разность главных
напряжений:
![]() (2.7)
(2.7)
где ![]() и
и ![]() для плоского напряженного состояния;
для плоского напряженного состояния; ![]() и
и ![]() для плоской деформации.
для плоской деформации.
|
|
|
Рис. 6. Характеристики образца для случаев просвечивания и отражения лучей света. |
Постоянная
с описывает изменение длины оптического пути в конкретном материале
при определенном напряженном состоянии. Поэтому постоянная с является
количественной мерой получаемого теневого оптического эффекта и называется
теневой оптической постоянной.
Влияние на изменение длины оптического пути
анизотропии материала ![]() характеризуется коэффициентом λ. Численные значения постоянных
А, В, п и определенных с их
помощью теневых оптических постоянных с и коэффициента анизотропии λ для разных материалов приведены в таблицах.
характеризуется коэффициентом λ. Численные значения постоянных
А, В, п и определенных с их
помощью теневых оптических постоянных с и коэффициента анизотропии λ для разных материалов приведены в таблицах.
Уравнения
(2.1), (2.2) и (2.7) описывают проецирование плоскости объекта на плоскость
изображения теневой оптической картины при произвольном распределении напряжений ![]() . Конкретное уравнение проецирования для
частной задачи
концентрации напряжений получается подстановкой в общее уравнение (2.7)
конкретных формул, характеризующих распределение напряжений в рассматриваемой
задаче.
. Конкретное уравнение проецирования для
частной задачи
концентрации напряжений получается подстановкой в общее уравнение (2.7)
конкретных формул, характеризующих распределение напряжений в рассматриваемой
задаче.
Уравнения проецирования и каустик для частных задач
Будут рассмотрены и сопоставлены три задачи концентрации напряжений (рис. 2.7): задача о действии сосредоточенной сжимающей силы Р на край полуплоскости (а); пластина с круглым отверстием, растянутая в двух направлениях усилиями р и q (б); растянутая пластина с трещиной при нагружении типа I и коэффициентом интенсивности напряжений KI (в).
Поля линейно-упругих напряжений в зонах концентрации для трех перечисленных задач характеризуются следующими уравнениями:
а) ![]()
б) 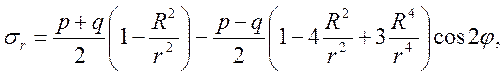

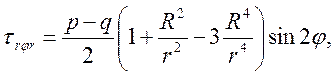
в) 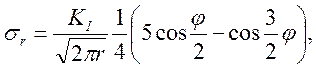
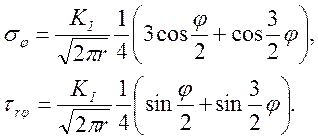
|
|
|
Рис. 7. Типичные задачи концентрации напряжений |
При таких распределениях напряжений с использованием уравнения (2.7; (для простоты рассмотрим лишь случай изотропии т. е. Я = 0) уравнения проецирования (9.1) и (9.2) принимают следующий вид:
а) при ![]()
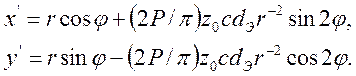
б) при ![]()
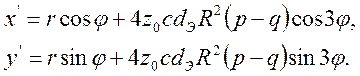
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.