Теневой оптический метод каустик – метод исследований напряжений и деформаций, страница 6

На образцах из прозрачных оптически анизотропных материалов (λ≠0) каустика раздваивается. На рис. 10 каустики вблизи вершины трещины в образце из оптически анизотропного материала аралдита В сравниваются с соответствующей единственной каустикой в образце из оптически изотропного материала. Поскольку коэффициент анизотропии λзависит от напряженного состояния (λ больше для плоской деформации, чем для плоского напряженного состояния, то расщепление двойной каустики больше для плоской деформации, чем для плоского напряженного состояния.

Рис. 10. Одна каустика для оптически изотропного материала (а) и двойная каустика для оптически анизотропного материала (аралдит В) (б).

Как внешняя, так и внутренняя каустика могут быть использованы для определения коэффициента интенсивности напряжений (КИН). Формула для определения КИН имеет следующий вид:

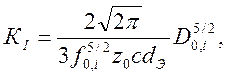                                                         (2.15)

где  диаметр наружной (внутренней) каустики вблизи кончика трещины;  – численный коэффициент при определении КИН с помощью наружной (внутренней) каустики. Величины коэффициентов  приближающиеся к 3,17 в случае единственной каустики, даны на рис. 11 в зависимости от коэффициента анизотропии λ. В двух других рассмотренных примерах (см. рис. 7) формулы для анизотропных материалов могут быть выведены аналогичным путем.

3. Каустики вблизи вершин трещин

Большинство приложений теневого оптического метода каустик до сих пор относилось к области механики разрушения. Поэтому теория каустик вблизи кончиков трещин была развита в наибольшей степени. В этом разделе приведены также некоторые результаты, представляющие более общий интерес и относящиеся к другим типам каустик.

Каустики вблизи трещин при нагружениях типов 1, II и III

Возможны три типа нагружения трещин (рис. 12): нагружение растяжением (тип I) (а), сдвиг в плоскости (тип II) (о) и антиплоский сдвиг (тип III) (в). Любое произвольное нагружение может быть представлено в виде суперпозиции этих трех основных типов нагружения.

Поскольку рассматриваются нагрузки как в плоскости, так и вне плоскости, необходимо использовать полные поля напряжений и перемещений в трех направлениях. Эти поля характеризуются следующими соотношениями:

а)  тип I:

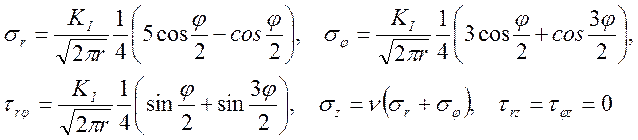
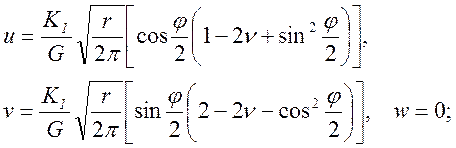
б)  тип II:

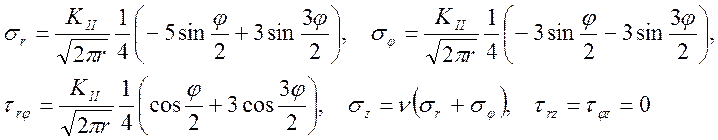
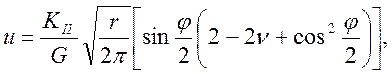                                                     (2.16)

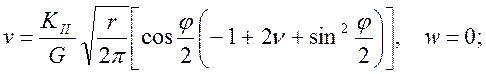
в)  тип III:

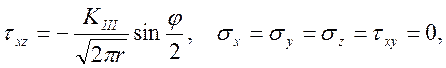
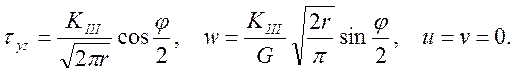
где  – модуль сдвига материала; u, v, w – перемещения в направлениях х, у, z;  – коэффициенты интенсивности напряжений типов I, II и III соответственно. Напряжение  и перемещения и и vв уравнениях для нагружений типов I и II даны для случая плоской деформации. Однако их можно легко преобразовать для случая плоского напряженного состояния, полагая  и заменив v на v/(1+v) в уравнениях для и и v.

12. Основные типы нагружения трещин.

Поскольку уравнения полей напряжений при нагружениях типов I и II по форме подобны, процедура определения каустик при нагружении типа II аналогична описанной в предыдущем разделе для случая трещин при нагружении типа I. Однако для нагружения типа III напряжения и перемещения в плоскости равны нулю и изменения длины оптического пути, согласно уравнению (2.7), также должны быть равны нулю. Физически нагружение вне плоскости не изменяет толщину пластины или (в случае просвечивания) показатель преломления материала.

Таким образом, теневой оптический эффект, соответствующий описанным выше эффектам, не имеет места. Однако для образования теневой картины может быть использовано перемещение, перпендикулярное к плоскости пластины w(x, у), но только при отражении. Изменение длины оптического пути в этом случае определяется по формуле

                                              (2.17)