Теневой оптический метод каустик – метод исследований напряжений и деформаций, страница 17

Остановка движущейся трещины достигается в образце с уменьшающимся коэффициентом интенсивности напряжений [например, в образце в виде двойной консольной балки (ДКБ),. нагружаемом с помощью клина (рис. 9.42)]. Трещина начинает двигаться от предварительно созданного выреза длиной а₀ при критическом перемещении 26. Вершина выреза скруглена, чтобы накопить достаточную упругую энергию в образце до начала движения трещины с целью ее ускорения до высокой скорости. В процессе движения трещины перемещение 26 остается постоянным вследствие значительной жесткости системы нагружения с помощью клина. Однако образец при увеличении длины трещины становится более податливым. Следовательно, интенсивность напряжений вблизи кончика трещины постепенно уменьшается с увеличением длины трещины, которая останавливается по достижении длины а_а. Был исследован процесс изменения КИН при распространении и остановке трещины в образцах ДКБ из аралдита В размером 321x127x10 мм.

На рис. 9.43 воспроизведена серия из шести фотографий теневых оптических картин, зарегистрированных с действительного изображения при просвечивании (г₀<;0). На каждой фотографии указано мгновенное положение кончика трещины. Можно видеть, что с увеличением длины трещины диаметр каустики уменьшается, что указывает на снижение КИН. Результаты, полученные с помощью фотографий с использованием формулы (9.15), представлены на рис. 9.44. На рисунке приведены результаты для трещин, начавших движение при разных величинах коэффициента интенсивности напряжений /Ск/. Приведены значения динамического КИН /С1^ДИН (точки) в зависимости от длины трещины а, а также графики зависимости от а соответствующего статического КИН /С:⁰¹. Значения статического КИН определяли измерением критического перемещения 26 с использованием обычной формулы для стационарной трещины [27]:

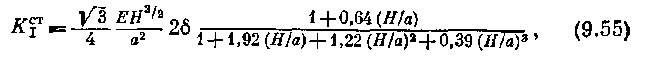
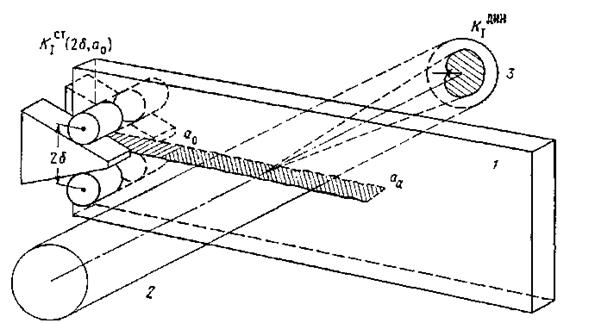
^;Рис. 9.42. Экспериментальная установка для исследования поведения останавливающихся трещин, / — образец ДКБ из аралдита В; 2 — освещающий пучок; 3 — плоскость изображения.

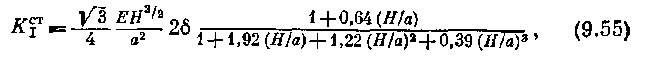
где Е—модуль упругости, 211 — высота образца, а — длина трещины. Кроме коэффициентов интспсшнюсти напряжений н нижней части рис. 9/14 показаны графики изменения скорости распространения трещин. С помощью этих данных могут быть определены следующие характеристики остановки трещин.

На начальной стадии движения трещины динамический КШ I /С^ин меньше соответствующей статической величины Л'Г'^Г. В конце движения трещины динамический коэффициент Лл^д"" больше соответствующей статической величины Лл^ст. Только

Рис. 9.43. Серия фотографии тепеиых картин д."!я распространяющейся и затем останавливающейся трещины (депстииIсльпые изображения при просвечивании образца из ара.чдита В).

после остановки динамический коэффициент Л'г¹"" приближается к статическому коэффициенту /vi,Л¹. Разница между графиками динамических и статических КПП меньше для трещин, начавших движение при более низких значениях К\_:1 п, таким образом, движущихся с более низкими скоростями. Динамические эффекты, очевидно, уменьшаются со снижением скоргк-тп, как п с лс дов ал о о ж 11 д а ть.

Поведение динамических коэффициентов интенсивности па-пряжений после остановки трещины для двух экспериментов показано на рис. 9.45. Приведены графики зависимости от времени / динамических КИП /С|^Д11И. Видно, что /С|^А"" колеблется

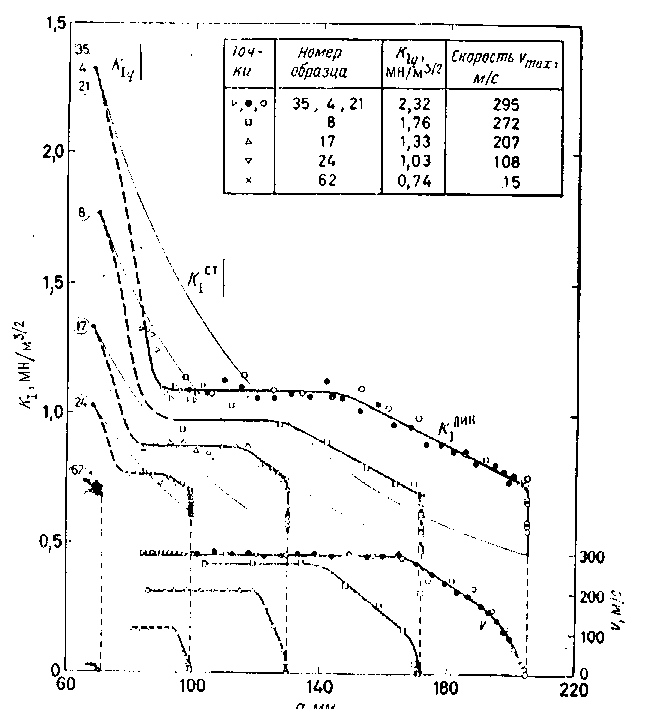
Рис. 9.'М. Измените КПП Л'] в процессе движения и остановки трещин в

зависимости ог длины трещин а.

около статической величины КИП при остановке трещины /Сь/¹. 1олы\о спустя достаточно большой промежуток времени после остановки трещины динамический КИМ приближается к с!атпческой величине.

Эти результаты показывают, что в момент остановки трещины динамическое напряженное состояние преобладает, хотя скорость трещины в этот момент равна нулю. Такое поведение трещины находится в соответствии с концепцией преобразования кинетической энергии [34]. При распространении трещины создаются упругие волны, в результате чего кинетическая энергия поглощается образцом. На ближних границах образца эти