Теневой оптический метод каустик – метод исследований напряжений и деформаций, страница 10

Упругой деформацией г^е можно пренебречь по сравнению с пластической деформацией е^р, так как е^е<§Се^р. Ввиду несжимаемости материала при пластической деформации (постоянства объема) имеем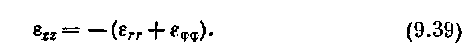

Следовательно, уравнения проецирования (9.1) и (9.2) принимают вид

Деформации в непосредственной окрестности кончика трещины были вычислены в работах [21—23]. Для идеального упруго-пластичного материала [т. е. для неупрочняющегося материала с п-+оо (рис. 9.23)] деформации не ограничены в веерообразной зоне (с углом —79,7°<;ф< +79,7°) перед кончиком трещины (рис. 9.24). Снаружи этой зоны деформации ограничены и имеют конечные значения. Количественно деформации характеризуются следующими выражениями:

Рис. 9.23. Диаграммы упруго-пластического деформирования	Рис. 9.24. Поле упруго-пластических деформаций

где / — величина так называемого /-интеграла, а ао — предел текучести материала на растяжение. С использованием уравнении (9.41) уравнения проецирования (9.40) принимают следую следующий вид:

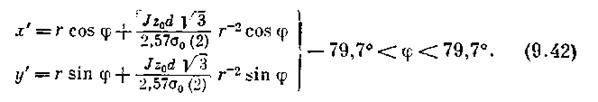
Ограниченные деформации снаружи веерообразной зоны (—79,7°<ф<; + 79₎7⁰) не влияют на каустику. С помощью соотношения (9.10) получаем следующее уравнение начальной кривой:

Эта кривая представляет собой окружность постоянного радиуса Го с центром в кончике трещины (однако она определена лишь в пределах сегмента —79,7°<;ф<;+ 79,7°). Проецирование начальной кривой (9.43) на плоскость регистрации с помощью уравнений (9.42) дает уравнения каустики:

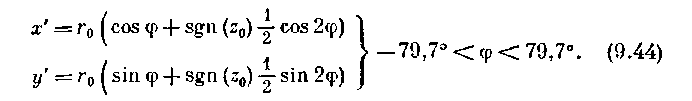
Форма каустики в плоскости регистрации z₀>0 показана на рис. 3.25. Аналогично упругому случаю характерным размером каустики является максимальный диаметр Dв направлении y, который связан с радиус начальной кривой:

                                    (3.45)

С использованием уравнений (9.43) и (9.45) находим

                          (3.46)

Это уравнение позволяет определить величину /-интеграла с помощью упруго-пластических каустик, образованных с использованием начальной кривой, расположенной вблизи кончика трещины при упруго-пластическом поле напряжений.

Для упрочняющегося материала [1<п<оо (рис. 9.23)] поле деформаций становится более сложным, и форму каустик уже нельзя вычислить аналитически. Однако картину распределения лучей света вокруг конца трещины в плоскости регистрации можно получить с помощью численных расчетов. Полученные таким образом результаты показаны на рис. 9.26 [7] для я = 25, 9, 3 и 1. Каустика видна как пограничная кривая между зонами нулевой (тень) и высокой интенсивности света.

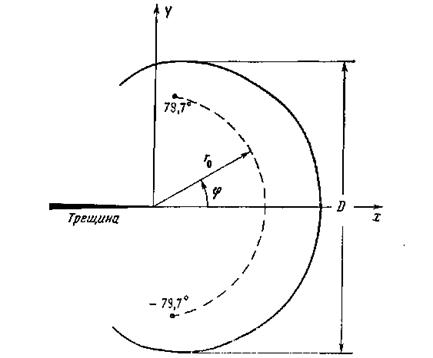
Рис. 9.25. Форма каустики и начальной кривой вблизи кончика трещины при упруго-пластических деформациях (п—>-оо) [6],

Можно видеть, что каустика при я = 25 близка к аналитически вычисленной каустике для неупрочняющегося материала («—»-оо). Кроме того, для предельного случая я=1 (упругий материал) полученная каустика такая же, как каустика вблизи кончика трещины в упругом материале. Формы каустик при «=3 и я = 9 занимают промежуточные положения между этими предельными случаями.

На рис. 9.27 показана фотография теневой картины при упруго-пластической деформации образца из инструментальной

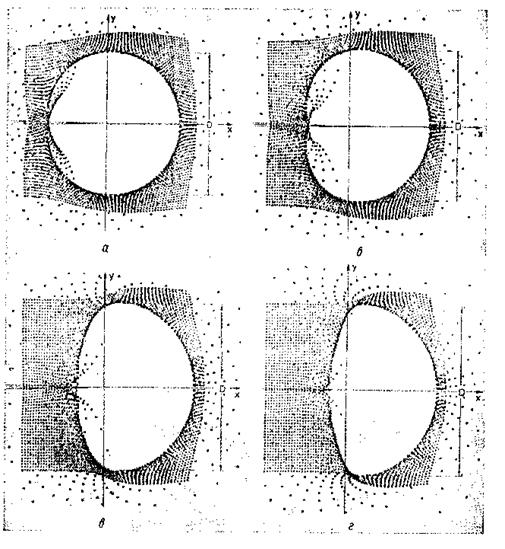
Рис. 9.26. Теневые зоны для трещины в упруго-пластическом материале при п, равном 1 (а), 3 (б), 9 (в) и 25 (г) [7].

стали, согласно которой можно заключить о низкой степени упрочнения материала. Несмотря на образование линий скольжения, которые нарушают условия отражения лучей света от полированной поверхности образца, теневая картина имеет высокое качество. Наблюдаемая форма каустики хорошо согласуется с теоретически предсказанной кривой и свидетельствует о применимости теневого оптического метода каустик для исследования задач концентрации пластических деформаций.

Рис. 9.27. Фотография теневой картины при упруго-пластической деформации [6].

9.4. Методика эксперимента