Теневой оптический метод каустик – метод исследований напряжений и деформаций, страница 8

При динамическом нагружении распределение напряжений вблизи кончика стационарной трещины такое же, как при статическом нагружении тела с трещиной . Однако величина КИН зависит от времени. Следовательно, поскольку зависимости от расстояния r и угла φ в динамическом и статическом случаях одинаковы, представленные в предыдущем разделе результаты применимы и к случаю динамически нагруженных трещин, если величины КИН /С_ь /Си и /Сш заменить на Кг^), /Сп(0 и/С_ш(0-

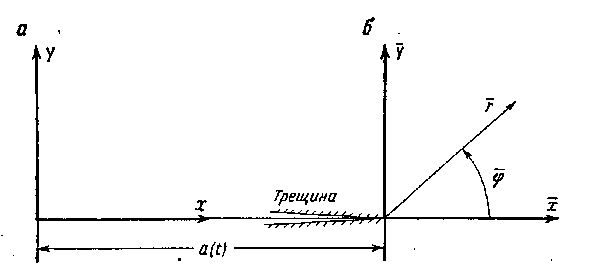
Рис. 9.18. Системы координат в кончике движущейся трещины: стационарная (а) и движущаяся (б).

Для трещины распределение напряжений вблизи кончика отличается от распределения вблизи стационарной трещины из-за инерционных эффектов [18, 19].

В системе координат (х, у) или (г, ср) с началом координат в кончике движущейся трещины (рис. 9.18)

(а — длина трещины) распределение напряжений вблизи трещины, движущейся с мгновенной скоростью ^ = д.а1(И характеризуется соотношениями:

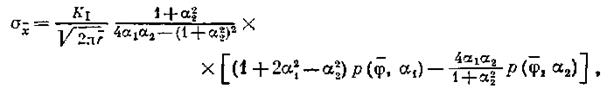
При таких упрощениях уравнение начальной кривой получается аналогичным статическому случаю |[см. уравнение (9.Ив) в разд. 9.2]:

Следовательно, получаем формулу

Таким образом, формула для определения величины КИН в случае движущейся трещины имеет такой же вид, как для стационарной трещины [см. уравнение (9.14в)], за исключением

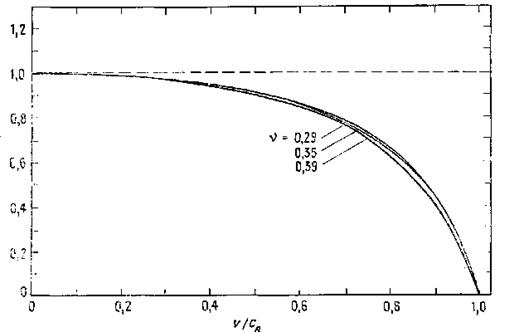
Рис. 9.19. Зависимость поправочного коэффициента Р от скорости трещины v(v — коэффициент Пуассона).

поправочного коэффициента Р^), который учитывает влияние скорости на распределение динамических напряжений в зависимости от г и ф вблизи движущейся трещины. Изменение коэффициента Р в зависимости от скорости трещины vизображено на рис. 9.19. Величина Р меньше 1 (при малых скоростях трещины он близок к 1).

На рис. 9.20 показаны формы каустик вблизи кончика трещины при различных скоростях трещины, но при одинаковой величине КИН. Скорость трещины отнесена к скорости волны Рэлея

Формы динамических каустик сопоставлены с формами статических каустик. Для всех скоростей роста трещин формы динамических и статических каустик практически одинаковы, однако размер динамических каустик несколько возрастает с увеличением скорости, что учитывается поправочным коэффициентом р.

Для каустик в оптически анизотропных материалах ситуация несколько усложняется, поскольку в уравнениях появляется дополнительный член, отражающий анизотропию, и образуются двойные каустики. Однако можно показать, что размер наружной каустики увеличивается с увеличением скорости тре-

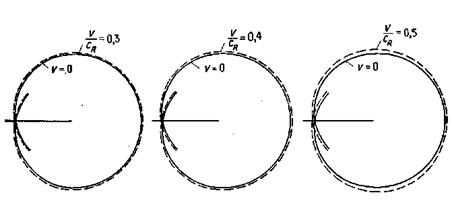
Рис. 9.20. Форма каустик для движущихся трещин в оптически изотропном материале (с_к — скорость волны Рэлея).

щины таким же образом, как и в случае единственной каустики для оптически изотропного материала [9]. Увеличение размера внутренней каустики с увеличением скорости трещины несколько больше, чем для единственной каустики. Таким образом, поправочный коэффициент Р(v) для изотропного материала, определяемый по формуле (9.30), дает хорошую аппроксимацию для случая двойной каустики, если его применять к наружной каустике.

Влияние на каустики эффектов высокого порядка

До сих пор рассматривалось только распределение напряжений в окрестности кончика трещины. Строго говоря, такое поле напряжений имеет место лишь при г->0, т. е. область примене-

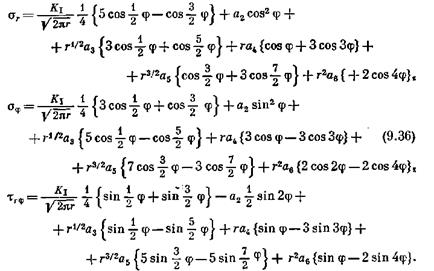
ния рассмотренных уравнений ограничена непосредственной окрестностью кончика трещины. В промежуточной и удаленной от кончика трещины зонах в уравнения, характеризующие распределение напряжений, необходимо включить члены рядов более высокого порядка. Поскольку каустика представляет собой проекцию начальной кривой с радиусом г₀ вокруг кончика трещины, эти члены высокого порядка могут оказывать влияние на форму каустики. В большинстве практических задач не рассматриваются длинные трещины в образцах большого размера. Однако для коротких трещин и для трещин, приближающихся к краю образца, влияние членов высокого порядка приходится учитывать. Полное решение, характеризующее поле напряжений вокруг кончика трещины, представляется в виде ряда, первый член которого дает распределение напряжений вблизи самого кончика. При растяжении тела с трещиной (на-гружение типа I) первые шесть членов ряда имеют следующий вид [20]: