в) при 
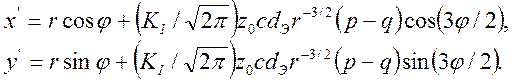
Полное семейство отклоненных лучей образует за плоскостью объекта теневую зону. Поверхность теневой зоны является огибающей лучей света и называется поверхностью каустики. Пересечение этой поверхности с плоскостью изображения образует каустику. Каустика определяется многозначным сингулярным решением уравнений (2.1) и (2.2) (т. е. точки проецирования лучей вдоль каустики не обратимы). Таким образом, необходимым и достаточным условием образования каустики является равенство нулю якобиана уравнений (2.1) и (2.2):
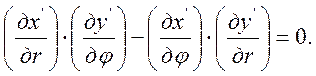(2.10)
Координаты r, φ точек P, которые удовлетворяют уравнению (2.10), образуют начальную кривую в плоскости объекта, а проекция этой начальной кривой на плоскость изображения есть каустика.
Следовательно, применив условие (2.10) к уравнениям проецирования (2.4), получим следующие уравнения начальных кривых:
а) 
при 
,
б) 
при , (2.11)
в) 
при
Для всех рассмотренных примеров начальные кривые представляют собой окружности постоянного радиуса r0 с центрами в точке концентрации напряжений. С помощью уравнений проецирования (2.9) получаем наконец уравнения каустик как изображений начальных кривых [уравнения (2.11)] в следующем виде:
а) при
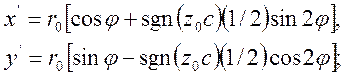
б) при
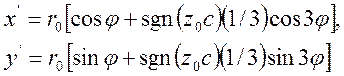(2.12)
в) при
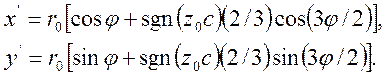
Математически каустики характеризуются уравнениями обобщенных эпициклоид. Форма каустик показана на рис. 8 для положительных и отрицательных величин расстояния го между образцом и плоскостью изображения.
Иллюстрацию
картины полного распределения отклоненных лучей света в плоскости изображения получаем
очень просто при рассмотрении проецирования лучей света от плоскости объекта вдоль линий 
. Изображения этих линий, полученные с помощью
уравнений (9.9) для трех рассмотренных примеров, показаны на рис. 9. Каустики видны как
огибающие семейства
линий изображения (см. для сравнения рис. 8).
|
|
|
|
Рис.8. Форма каустик для рассмотренных задач концентрации напряжении. |
Рис 9. Распределение света на теневых картинах для рассмотренных задач концентрации напряжений: а—сжимающая сосредоточенная сила на краю полуплоскости; б — пластина с круглым отверстием при двухосном растяжении; в –трещина в пластине при нагружении типа I. |
Для количественной характеристики каустик вводится параметр длины, определяемый расстоянием между характерными точками каустик; им может быть, например, максимальный диаметр каустики Dна рис. 8. Этот диаметр связан с радиусами начальных кривых следующими соотношениями:
(2.13)
С помощью уравнений (2.11) и (2.13) получаем формулы, связывающие размер теневой оптической картины с параметром нагружения:
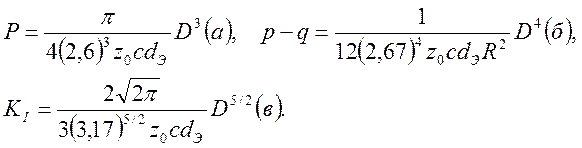(2.14)
Таким образом, с помощью уравнений (2.14) и экспериментально измеренных диаметров каустик D можно определить параметр нагружения, т.е. величину сжимающей сосредоточенной силы в случае а, разность главных номинальных напряжений p-q в случае б и коэффициент интенсивности напряжений КI в случае в.
Можно также использовать и другие характерные размеры каустик, отличные от показанных на рис. 8, а также рассматривать каустики, полученные в плоскостях регистрации противоположного знака. Однако, чтобы получить практичные и достаточно точные формулы для количественной оценки, желательно выбрать каустику, имеющую наибольший измеряемый размер между характерными точками. Кроме того, характерные точки должны лежать на самой каустике. Следует избегать использования характерных точек, расположенных не на каустике (например, на контуре образца). В процессе образования теневой картины такие точки нечетко воспроизводятся и не могут быть установлены с достаточной точностью. Некоторые точки, расположенные на каустике, при детальном рассмотрении все же оказываются неподходящими для измерений, такие, например, как точки излома каустик на рис. 8. Диаграммы распределения лучей света (рис. 9) показывают, что положение таких точек экспериментально устанавливается с невысокой точностью из-за их фокусирующего характера. Поэтому на основе предварительного анализа в качестве примерного размера был выбран диаметр каустики D, показанный на рис. 8.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
