Электромагнитные поля и волны. Часть 2 (Направляющие системы СВЧ-диапазона. Регулярные волноводы. Колебательные системы СВЧ. Общая теория цепей СВЧ), страница 4

Любая регулярная линия передачи обладает неизменным поперечным сечением и прямолинейной продольной осью Z, вдоль которой может распространяться электромагнитная волна. Вследствие этого, зависимость поля от поперечных координат X и Y должна быть одинакова во всех поперечных сечениях, а с изменением Z могут изменятся лишь фазы и амплитуды поля. Отсюда решение уравнения ищется в виде:

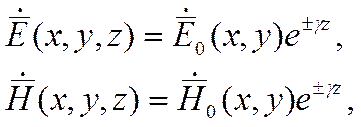                                                                     (2.2)

где γ – коэффициент распространения, в общем случае есть комплексная величина: , α – коэффициент затухания, β – коэффициент фазы. Наличие у γ мнимой части указывает на распространяющую ЭМВ, при этом описывает падающие волны, распространяющие в направлении возрастания координаты Z, а  - в сторону убывание Z, то есть отраженную ЭМВ.

Для отыскания решения поперечные составляющие (x, y), (x, y) выражают через продольные (z), (z), которые удовлетворяют волновым уравнениям:

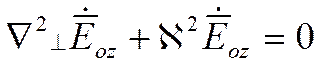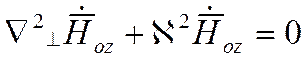              ; .              (2.3)

здесь  - двумерный оператор Лапласа по поперечным координатам.

Для определения поля в линии передачи нужно удовлетворить граничным условиям на поверхности раздела, то есть касательная к металлической поверхности вектора 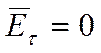, и нормальная вектора .

Решение уравнений (2.3) возможно только при строго определенных дискретных, вещественных, положительных значениях  , которые называют собственными числами. Они определяются формой и размерами поперечного сечения волновода. Каждому собственному числу  соответствует функция, удовлетворяющая уравнению и определяет ЭМП конкретного типа E и H. Конкретный тип поля E или H имеет свой коэффициент распространения: 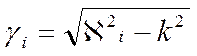 (2.4), где .

Поскольку собственные числа  представляют собой бесконечный ряд чисел, то и ЭМП типа Е и Н также есть бесконечный ряд типов волн Е и Н в волноводах. Результирующее поле в волноводе в общем случае представляет собой бесконечную сумму полей всех возможных типов, которые могут распространятся в данном волноводе.

Далее будем рассматривать волноводы без потерь, что упрощает решение задачи, то есть коэффициент затухания . Тогда коэффициент распространения  может быть либо мнимым числом, либо вещественным.

Если   - мнимое число – в волноводе существует бегущая ЭМВ,  - вещественное число, - в волноводе будет существовать затухающая ЭМВ без сдвига по фазе, она не переносит энергию и информацию.

Плоские бегущие волны. При этом  , из уравнения  следует, что , Тогда  и в волноводе будут существовать бегущие ЭМВ по оси z, амплитуды которых не зависят от z, а определяются координатами X и Y. Фазовый фронт ЭМВ представляет плоскую поверхность, перпендикулярную направлению, распространения ЭМВ. Амплитуды векторов  и  в плоскости фронта неодинаковы, такую волну называют неоднородной плоской.

Отношение комплексных амплитуд поперечных составляющих  электрического поля и  магнитного поля, имеющее размерность сопротивления, называют характеристическим сопротивлением поля .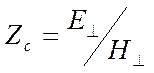

Для поля типа Е волновое сопротивление Z_с равное

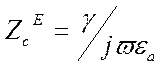
при   чисто вещественное и равно

,

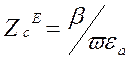а для поля типа Н равно

.

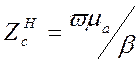Связь между векторами  и  осуществляется через Z_с, а волновые сопротивления для типов волны Е и Н чисто вещественные, то и изменяются в фазе и таким образом энергия переносится максимально в продольном направлении (по оси z). Таким образом, при   в волноводе существует неоднородная плоская бегущая волна типа Е или типа Н, или обе вместе.

Местные затухающие поля. При  коэффициент распространения γ является вещественной величиной: 

.

Из (2.2) следует, что

.

В этом случае каждый из векторов поля в любой момент времени имеет фазу одинаковую во всех точках волновода, амплитуды векторов поля затухают в направлении z по экспоненциальному закону . Характеристические сопротивления  и  оказываются мнимыми, а векторы   и  сдвинутыми по фазе на , что приводит к колебательному характеру движения энергии, то есть к отсутствию ее переноса вдоль волновода().