Квантовые статистики и их применения

2.2. Квантовые статистики и их применения

2.2.1. Краткие теоретические сведения

Согласно квантовой теории все микрочастицы подразделяют на два класса, которые описываются двумя  квантовыми статистиками:

Частицы с полуцелым спином называют фермионами; они подчиняются статистике Ферми-Дирака;

Частицы с целым спином – бозоны подчиняются статистике Бозе-Эйнштейна.

          В квантовых статистиках тождественные частицы принципиально неразличимы.

В статистике Ферми-Дирака в каждом квантовом состоянии может находиться не более одной частицы (принцип Паули), а в статистике Бозе-Эйнштейна – любое число частиц.

Для описания состояния системы частиц рассматривают во­ображаемое шестимерное пространство, каждая точка которого характеризуется шестью координатами: х, у, z, р_х, р_y, р_z. Это фазовое пространство. Согласно принципу неопределенностей Гейзенберга,  xp_x³ h,  Поэтому данному состоянию части­цы в фазовом пространстве соответствует не точка, а фазовая ячейка, объем которой

 .

Квантовые распределения представля­ют собой функции , определяющие средние числа частиц в одной фазовой ячейке с энергией , или функции заполнения ячеек имеют вид:

         для фермионов,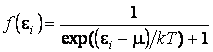      

         для бозонов                                  .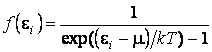

       Здесь m – так называемый химический потенциал. Для бозонов значения  не могут быть положительными, для бозонов m < 0. У макроси­стем с переменным числом бозонов (к числу которых относят­ся, например, фотоны) m = 0, и формула переходит в 

.

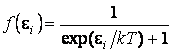Объем dL фазового шестимерного пространства для независимых частиц . Число фазовых ячеек в этом элементе объема получим, разделив   на объем одной фазовой ячейки, равный ,

,

Число ча­стиц dn в данном интервале энергий (в расчете на единицу объ­ема газа):                                  ,

 где - числовой коэффициент, зависящий от природы частиц.

Распределение Ферми-Дирака для  электронов в металле при температуре
Т = 0 К приведено на рис. 2.2.1 и имеет вид:

.

     Величину m называют энергией или уровнем Ферми: Е = m.  Эта энергия яв­ляется максимальной, которую могут иметь свободные элект­роны в металле при T= 0 К,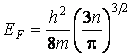. Энергия Ферми, как показывает расчет, слабо зависит от температуры:

.

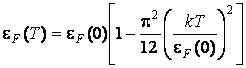  Число свободных электронов dn в интервале энергий  равно .                                                                                                                                                                                                                                                                                                                   Коэффициент  появился в связи с тем, что в каждой фазовой ячейке могут расположиться два электрона (фермиона) с про­тивоположно направленными спинами. При Т = 0 свободные электроны заполняют полностью (f = 1) все кванто­вые состояния с энергиями e < m.