Квантовые статистики и их применения, страница 6

ДАНО:

?

АНАЛИЗ. Фотонный газ подчиняется статистике Бозе-Эйнштейна. Число фотонов в полости в полости должно быть таким, чтобы их энергия была минимальной, т.е. . Функция распределения Бозе-Эйнштейна в этом случае принимает вид: 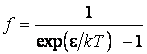. Для фотонов энергия , импульс , поэтому число возможных квантовых состояний (фазовых ячеек) равно:

.

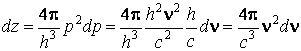Число фотонов с частотами, заключенными  в интервале ; ,  равно

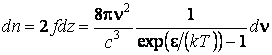.                                          (2.2.12)

Коэффициент 2 соответствует двум независимым поляризациям излучения во взаимно перпендикулярных плоскостях. Энергия этих фотонов , спектральная плотность энергии излучения (фотонного газа) . Подставив , найдём формулу Планка.

РЕШЕНИЕ. Энергия фотонов, частоты которых заключены в интервале , равна 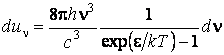 , тогда спектральная плотность энергии

.

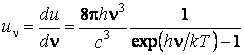Это и есть формула Планка. Для циклической частоты ω получаем

,

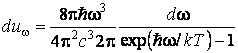и      .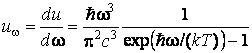

Проверим размерность: .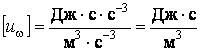

ОТВЕТ: .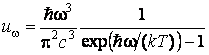

ЗАДАЧА 5. Определить максимальные значения энергии и импульса фонона в меди, дебаевская температура  = 330 К, плотность ρ = 8,9∙10³ кг/м³.

ДАНО:    = 330 К μ = 63,5∙10–3 кг/моль ρ =8,9∙103 кг/м3

εmax, рmax –?

АНАЛИЗ. Упругую волну в кристалле можно представить как совокупность квазичастиц-фононов, распространяющихся со скоростью u, равной скорости волны в кристалле. Фонон имеет спин, равный нулю, поэтому подчиняется статистике  Бозе-Эйнштейна. Фононный газ – система с  переменным числом частиц, его химический потенциал μ = 0.

Фонон обладает энергией  и импульсом , максимальные значения которых достигаются при температуре Дебая : .

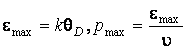РЕШЕНИЕ. Максимальная энергия фонона

.

Максимальный импульс фонона найдём как , где
λ_min – наименьшая длина волны фонона,  λ_min , где d – параметр кристаллической решётки, равный среднему расстоянию между атомами.