Проверим размерность 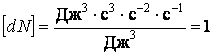 .
.
ОТВЕТ: 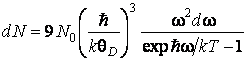 .
.
ЗАДАЧА 7. Оценить
давление: а) электронного газа на стенки в металле при Т = 0 К и
концентрации свободных электронов n =
2,5∙1022 см–3; б) теплового излучения в полости при
температуре Т = 330 К; в) фононного газа в меди с дебаевской
температурой ![]() = 330 К и концентрацией атомов
= 330 К и концентрацией атомов ![]() = 8,4∙1022 см–3.
= 8,4∙1022 см–3.
|
ДАНО: а) Т = 0 К, n = 2,5∙1028 м–3 б) Т = 330 К в)
|
|
|
АНАЛИЗ. Газ фермионов (электронов)
и газ бозонов (фотоны, фононы) рассматриваем как идеальный газ с той лишь
разницей, что вместо распределения Максвелла – Больцмана этот газ подчиняется
соответственно статистике Ферми-Дирака (электроны) или Бозе-Эйнштейна (фотоны,
фононы). Поэтому для определения давления газа будем использовать основное
уравнение МКТ ![]() =
=![]() n<ε>, где n – концентрация частиц (электронов, фотонов или
фононов), <ε> – средняя энергия частицы.
n<ε>, где n – концентрация частиц (электронов, фотонов или
фононов), <ε> – средняя энергия частицы.
РЕШЕНИЕ. а) найдём давление
электронного газа. Согласно формуле (2.2.9) задачи 1 средняя энергия электрона
<ε>=![]() ,
, 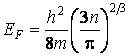 .
Тогда
.
Тогда
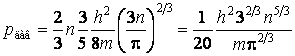 .
.
Проверим размерность:
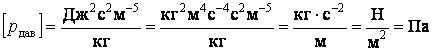 .
Подставим значения:
.
Подставим значения:
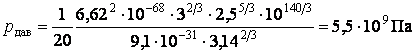 .
.
б) Найдём давление
фотонного газа в полости при Т = 330 К. Для равновесного фотонного газа
давление связано с плотностью энергии соотношением: ![]() ,
где
,
где 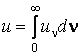 ,
, ![]() –
спектральная плотность энергии фотонного газа, определённая формулой Планка:
–
спектральная плотность энергии фотонного газа, определённая формулой Планка:
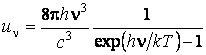 .
.
Проинтегрировав эту формулу по всем частотам от 0 до ∞, получаем
![]() ,
,
где ![]()
![]() – энергетическая светимость при
данной температуре,
– энергетическая светимость при
данной температуре, ![]() – постоянная
Стефана-Больцмана, с – скорость света.
– постоянная
Стефана-Больцмана, с – скорость света.
Давление фотонного газа
![]() .
.
Проверим размерность: 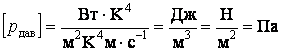 . Подставим значения:
. Подставим значения: 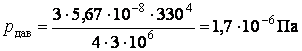 .
.
в) Найдём давление
фононного газа в меди. Учтём, что ![]() – энергия единицы
объёма фононного газа,
– энергия единицы
объёма фононного газа, 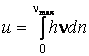 . Из формулы (2.2.13)
задачи 6
. Из формулы (2.2.13)
задачи 6
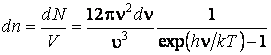 ,
,
тогда 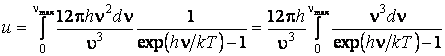 ,
причём
,
причём 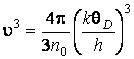 (см. задачу 6). Подставив
(см. задачу 6). Подставив ![]() , получаем
, получаем
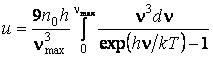 ,
и давление
,
и давление 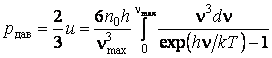 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.