Квантовые статистики и их применения, страница 4

Учитывая, что Е_F = , получаем:

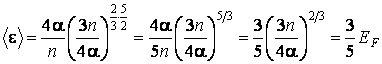 .           (2.2.9)

Проверим размерность: .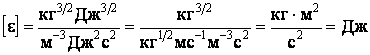

         Найдём вероятность обнаружить электрон с энергией в интервале  – Δε;  + Δε при температуре Т > 0 К.  Для этого получим распределение Ферми-Дирака при Т > 0, подставив в выражение (2.2.5) функции (2.2.1) и (2.2.4):

.

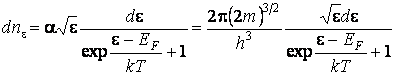Искомая вероятность , где n – концентрация свободных электронов в металле.

Для определения энергии Ферми необходимо использовать формулу

.

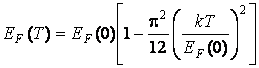Вычислим (0) по формуле (2.2.8):

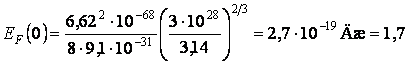эВ.

При Т = 100 К получим: ,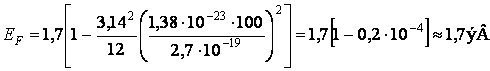

при  Т = 1000 К найдем:

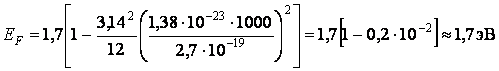
– можно считать, что при Т = 100 К  и при Т = 1000 К  уровень Ферми не отличается от  (0). Средняя энергия свободных электронов эВ.

         Число частиц n в единице объёма найдём, проинтегрировав  по всем значениям энергии от 0 до  . Так как при изменении температуры концентрация свободных электронов в металле не меняется, интегрирование можно проводить для Т = 0 К и  воспользоваться результатом (2.2.7), тогда  вероятность

.

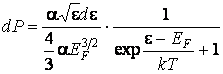Заменим , получаем

,

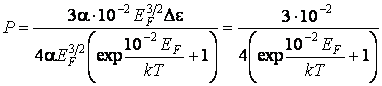При Т = 100 К   .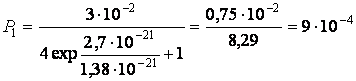

При Т = 1000 К  .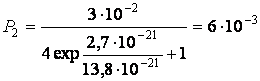

ОТВЕТ: 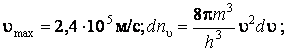 Е_F(0) = 1,7эВ; <ε>=.

ЗАДАЧА 2. Вычислить интервал между соседними энергетическими уровнями свободных электронов в металле при Т = 0 К вблизи уровня Ферми. Концентрация свободных электронов 10²² см^–3 , объём металла V = 3 см³.

ДАНО: V = м3    Т = 0 К        п = 1028 м–3

δε – ?

АНАЛИЗ. Электроны в металле подчиняется принципу запрета Паули, согласно которому в одном квантовом состоянии  (одной фазовой ячейке)  может находится не более двух электронов с противоположно направленными спинами, т.е.  = 2. При температуре Т = 0 К и энергии электронов ε ≤ функция распределения , свободные электроны заполняют все квантовые состояния, поэтому число электронов с энергиями в интервале  ( – интервал между соседними энергетическими уровнями) равно 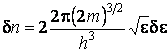. В связи с малостью δε мы приняли δε.