Распределение Бозе-Эйнштейна для фотонного и фононного газов приведено на рис. 2.2.2, где сплошной линией изображено распределение Бозе-Эйнштейна, пунктиром – Максвелла – Больцмана:
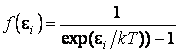 .
.
|
рис. 2.2.2 |
Для фотонов e = hn и р=hn/c, поэтому число квантовых состояний (фазовых ячеек) в интервале частот (n, n + dn)в расчете на единицу объема фотонного газа равно
![]() .
.
Число фотонов с частотами в интервале (n, n + dn) равно
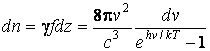 .
.
Коэффициент ![]() соответствует двум возможным поперечным
поляризациям фотона. Спектральная плотность энергии излучения
(фотонного газа)
соответствует двум возможным поперечным
поляризациям фотона. Спектральная плотность энергии излучения
(фотонного газа)
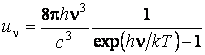 .
.
Это формула Планка.
Для фононов число квантовых состояний (фазовых ячеек) в интервале частот (n, n + dn)в расчете на единицу объема
![]()
где ![]() скорость акустических волн
в кристалле.
скорость акустических волн
в кристалле.
Фонон имеет три
поляризации (продольную и две поперечные), поэтому коэффициент ![]() . Максимальная энергия фонона
достигается при температуре Дебая
. Максимальная энергия фонона
достигается при температуре Дебая ![]() .
.
2.2.2. Примеры решения задач
ЗАДАЧА 1. Пользуясь
распределением Ферми-Дирака, найти а) функцию распределения электронов по
скоростям и их максимальную скорость при
Т = 0 К, значение энергии Ферми ![]() ;
б) среднюю энергию свободных электронов при этой температуре; в) вероятность
обнаружить электрон с энергией в интервале от
;
б) среднюю энергию свободных электронов при этой температуре; в) вероятность
обнаружить электрон с энергией в интервале от ![]() -
0,01
-
0,01![]() до
до ![]() +0,01
+0,01![]() при температуре 100 К, при 1000 К.
Концентрация свободных электронов n = 3∙1022 см–3.
при температуре 100 К, при 1000 К.
Концентрация свободных электронов n = 3∙1022 см–3.
|
ДАНО: а) Т = 0 К; в) ε =
п = 3∙1028 м–3 |
|
а) d n ( б) <ε> – ? в) Р1; Р2 – ? |
АНАЛИЗ. Для решения задачи воспользуемся распределением Ферми-Дирака:
![]()
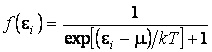 .
(2.2.1)
.
(2.2.1)
При абсолютном нуле (Т = 0 К) величина μ есть энергия Ферми (μ=ЕF), это максимальная энергия, которую может иметь электрон в металле.
Электрон в металле движется как свободный, его полная энергия равна кинетической, т.е.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.