Квантовые статистики и их применения, страница 5

         Обозначив 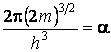, получаем  ,  или при

2 = 2.                                                (2.2.10)

Решив это уравнение относительно δε находим дискретность уравнений энергии электронов в металле.

РЕШЕНИЕ. Из формулы (2.2.10) получаем . Подставив в эту формулу, значение 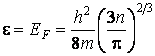, имеем

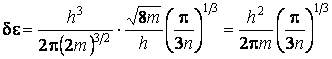.                   (2.2.11)

Проверим размерность: .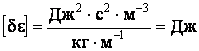

При проверки размерности мы домножили размерность правой части выражения (2.2.11) на м^–3 в связи с тем, что при подстановке м^–3 размерность величины  была опущена.

Подставим значения:

.

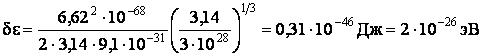– дискретность уровней весьма мала. Её обнаружить практически невозможно, поэтому спектр электронов в металле рассматриваем как квазинепрерывный.

ОТВЕТ: .

ЗАДАЧА 3.Найти функцию распределения  свободных электронов в металле при Т = 0 К по длинам волн де Бройля в расчёте на единицу объёма. Оценить минимальную длину волны де Бройля при концентрации свободных электронов  n= 10²² см^–3.

ДАНО: Т = 0 К  n = 1028 м–3

; λmin – ?

АНАЛИЗ. Чтобы найти функцию распределения электронов по дебройлевским длинам волн, необходимо перейти от функции  к функции , где – длина волны де Бройля соответствующей частицы, р – импульс частицы.

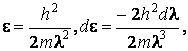
РЕШЕНИЕ. В функцию распределения = подставим  Получаем    знак «минус» указывает, что при .  Учитывая, что - это вероятность (величина постоянная), отбросим «минус» как не имеющий физического смысла:

.

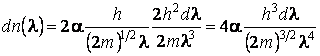Подставив  имеем:  .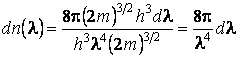

Проверим размерность:  .

Минимальное значение волны де Бройля соответствует энергии Ферми: 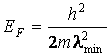, тогда 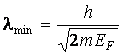. Подставив 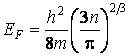, имеем:

.

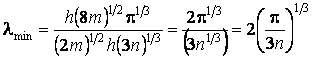Проверим размерность: . Подставим значения:

.

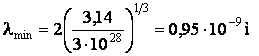ОТВЕТ: .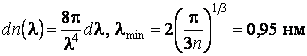

ЗАДАЧА 4.Пользуясь распределением Бозе-Эйнштейна, получить формулу Планка.