Квантовые статистики и их применения, страница 7

         Очевидно, при плотной упаковке концентрация атомов равна , где d³ – объём, занимаемый одним атомом в кристалле. Согласно МКТ,  , где М – молярная масса. Тогда 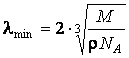, и  .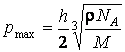

Проверим размерность 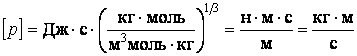. Подставим значения: .

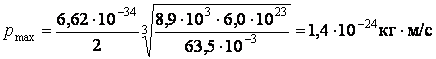ОТВЕТ. .

ЗАДАЧА 6.Кристалл состоит из  одинаковых атомов. Температура Дебая равна . Найти число dNфононов в интервале частот  при температуре кристалла Т.

ДАНО: п0, ,

dN – ?

АНАЛИЗ. Фононный газ описывается распределением Бозе-Эйнштейна

.

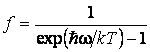Число фазовых ячеек (квантовых состояний) в пространстве импульсов равно: 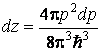, где  – объём оболочки сферы радиуса р и толщины  в пространстве импульсов,  – объём фазовой ячейки,  – постоянная Планка.

          В твердых телах могут распространяться три волны – одна продольная и две поперечные с двумя взаимно перпендикулярными поляризациями, поэтому концентрация фононов в интервале частот  равна   ,  где
γ = 3. Учитывая, что импульс фонона , причём длина волны , получаем

.

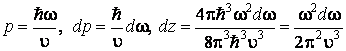Число фононов в данном интервале частот , где V – объём кристалла.

РЕШЕНИЕ. Подставив  в выражение для , имеем:

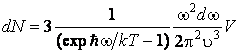.                                  (2.2.13)

Чтобы найти число фононов , в выражении (2.2.13) исключим скорость . Для этого учтём, что полное число квантовых состояний фононного газа с учётом трёх поляризаций фонона равно числу степеней свободы 3 , где  – концентрация атомов:

.

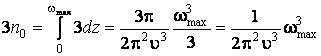Отсюда .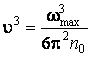

          Максимальная частота фонона достигается при температуре Дебая , тогда  ,  и 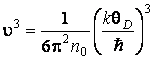. Подставив в (2.2.13), получаем

.

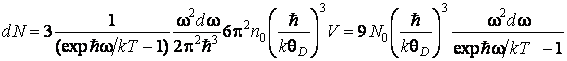Здесь  –  число атомов в кристалле.