Элементы кристаллографии

Различают дефекты точечные (примесные атомы, вакансии), линейные (дислокации), плоские (границы кристалла, мозаичная структура), объемные (в частности поры), сложные.

Индексы направления задаются координатами ближайшего к началу координат узла. Координаты узла выражаются в единицах периодов решетки
a, b, c. Индексы направления записываются в квадратных скобках . Для отрицательного индекса знак «минус» ставится над индексом, например, .

Символ [111] указывает направление пространственной диагонали. У куба три пространственные диагонали, по условиям симметрии эти направления являются эквивалентными. Совокупность эквивалентных направлений образует систему направлений <111>. Следует иметь в виду, что индексы  задают не одну прямую, а семейство параллельных прямых (рис. 3.2.1).

Аналогично кристаллографические плоскости также задаются тройкой индексов , которые принято называть индексами Миллера. Индексы Миллера вводятся следующим образом. Пусть кристаллографическая плоскость отсекает на осях координат отрезки . Тогда уравнение этой плоскости в отрезках запишется так: 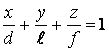. Если привести все члены уравнения к общему знаменателю и освободиться от него, то получим:

,

коэффициенты в этом уравнении и представляют систему индексов Миллера . Отрицательный знак индекса отмечается чертой над индексом, например . Эквивалентные плоскости составляют семейство . Так, для кубической решетки грани куба являются эквивалентными плоскостями, и семейство  представляет плоскости (100), (010), (001),    (рис. 3.2.2).

Молярный объем кристалла  , – молярная масса вещества;     – плотность.

Объем элементарной ячейки кубической решетки ; гексагональной решетки .

Число атомов в единице объема вещества         , где  – число атомов в одной элементарной ячейке.

Параметр кубической решетки .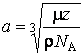

3.2.2. Примеры решения задач

ЗАДАЧА 1. Определить период кристаллической решетки алюминия, если известно, что его плотность , молярная масса  По рентгеноструктурным данным известно, что алюминий имеет гранецентрированную кубическую решетку (ГЦК-решетку, рис.3.2.3).