Элементы кристаллографии, страница 3

Третья координационная сфера имеет радиус, равный расстоянию от точки О до атомов, находящихся в центрах граней, которые не сходятся в точке О. Очевидно,  т. е. . Таких атомов в данной ячейке 3 ( А₇, А₈, А₉), в расчете на все окружение точки О, их будет .

Четвертая координационная сфера имеет радиус, равный диагонали грани . На ней будет размещаться столько же атомов, сколько и на первой координационной сфере – 12 ( А₉, А₁₀, А₁₁).

Пятая координационная сфера имеет радиус , равный расстоянию от точки О до атома, находящегося в центре грани соседней ячейки. На эту сферу попадает по 3 атома из восьми соседних ячеек: атома.

Шестая координационная сфера имеет радиус , равный пространственной диагонали куба. На ней будет находится   атомов (А₁₂).

Функция радиального распределения приведена на рис.3.2.5.

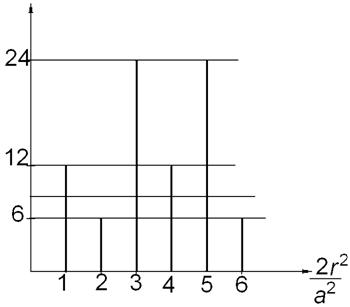
Рис. 3.2.5

ОТВЕТ: Радиальное распределение атомов в кубической гранецентрированной решетке:

ЗАДАЧА 3. Элементарная ячейка простой кубической решетки построена из одинаковых атомов, представляющих собой как бы жесткие шары с радиусом . Ребро элементарной ячейки . Показать, что при таком расположении атомы занимают часть объема, равную .

АНАЛИЗ. Простая кубическая структура является одной из самых рыхлых структур. Внутренняя полость структуры занимает достаточно большой объем. Объем элементарной ячейки . Для решения задачи необходимо определить, сколько атомов приходится на одну элементарную ячейку.

РЕШЕНИЕ. Каждый атом принадлежит одновременно восьми элементарным ячейкам, поэтому на одну ячейку приходится  атом. Согласно условию задачи объем элементарной ячейки . Заполненный в ячейке объем  равен объему атома: . Найдем отношение: