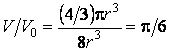 .
.
Таким образом,
плотность упаковки частицами пространства внутри вещества составляет ![]() .
.
ОТВЕТ: ![]() .
.
ЗАДАЧА 4. Определить
отрезки, отсекаемые на осях пространственной решетки плоскостью, заданной
индексами Миллера ![]() .
.
|
ДАНО: индексы Миллера
|
|
А, В, С – ? |
АНАЛИЗ. Данная задача на основы кристаллографии. За единицы измерения
отрезков на координатных осях приняты периоды кристаллической решетки ![]() .
.
РЕШЕНИЕ. Запишем величины, обратные индексам плоскости ![]() . Общий знаменатель дробей 10. Умножим
дроби на общий знаменатель. Полученные числа определяют искомые отрезки
. Общий знаменатель дробей 10. Умножим
дроби на общий знаменатель. Полученные числа определяют искомые отрезки ![]() .
.
ОТВЕТ: ![]() .
.
ЗАДАЧА 5. Какое наибольшее число линий может быть получено на
рентгенограмме, снятой на излучении с длиной волны ![]() Å
от кристалла простой кубической системы с параметром решетки
Å
от кристалла простой кубической системы с параметром решетки ![]() Å.
Å.
|
ДАНО:
|
|
АНАЛИЗ. Кристаллографические плоскости можно рассматривать как плоскости,
зеркально отражающие рентгеновские лучи. Расстояние d между параллельными плоскостями с индексами Миллера (![]() ) для кубической системы
) для кубической системы
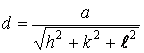 ,
,
|
Рис. 3.2.7 |
Между лучами 1 и 1¢, падающими
под углом скольжения θ, возникает разность хода ![]() (рис.
3.2.7). При условии
(рис.
3.2.7). При условии ![]() наблюдается максимум
первого порядка, который и фиксируется на рентгенограмме. Предполагается, что
образец имеет поликристаллическую структуру, и на его поверхность выходят
плоскости с разными индексами
наблюдается максимум
первого порядка, который и фиксируется на рентгенограмме. Предполагается, что
образец имеет поликристаллическую структуру, и на его поверхность выходят
плоскости с разными индексами ![]() , а, следовательно,
и
, а, следовательно,
и ![]() . Необходимо выделить все возможные
решения, вытекающие из условия
. Необходимо выделить все возможные
решения, вытекающие из условия ![]() .
.
Очевидно, что ![]() , а, следовательно,
, а, следовательно, ![]() . В нашем случае
. В нашем случае 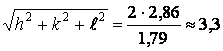 . Откуда
. Откуда ![]() .
Составим таблицу возможных комбинаций
.
Составим таблицу возможных комбинаций ![]() .
.
Таблица
возможных комбинаций индексов Миллера ![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
9 |
9 |
10 |
11 |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.