Элементы кристаллографии, страница 2

АНАЛИЗ. На рисунке схематически представлена элементарная ячейка алюминия. Она относится к типу гранецентрированных кубических решеток Браве, в которых атомы расположены в вершинах и центрах граней решетки. Каждый из атомов в данную элементарную ячейку входит лишь частично, т. к.  он входит в группу соседних элементарных ячеек. Атом, находящийся в вершине ячейки, в данную элементарную ячейку входит лишь на 1/8 своего объема, поскольку в вершине сходятся 8 смежных элементарных ячеек. Атомы, расположенные в центрах граней, одновременно принадлежат двум смежным ячейкам. Отсюда следует, что число атомов, входящих в данную элементарную ячейку, равно:

.

РЕШЕНИЕ. Объем элементарной ячейки . Объем одного моля вещества . Эту же величину можно выразить и другим способом:  (m – молярная масса вещества). Тогда  и   .

Проверка размерности: .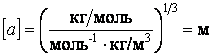

Расчет:   .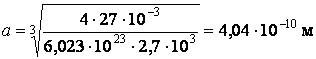

ОТВЕТ: .

ЗАДАЧА 2. Построить функцию радиального распределения частиц для гранецентрированной кубической решетки в зависимости от , где r – радиус координационной сферы, a – параметр решетки. Ограничиться шестью первыми координационными сферами.

АНАЛИЗ: Существенным признаком кристаллического состояния вещества является дальний порядок в размещении частиц тела, дающий возможность опираться на геометрические симметрии распределения частиц в пространстве и возможность использования для его характеристики пространственных решеток. Для характеристики закона распределения частиц в кристалле пользуются функцией распределения, значение которой равно числу частиц, находящихся на некотором расстоянии от какой-либо фиксированной точки. Эти частицы образуют координационную сферу. Важно отметить, что функция распределения частиц в кристаллах является дискретной, тогда как в жидкостях – непрерывной.

РЕШЕНИЕ. Выберем за исходную точку О, рис.3.2.4. совпадающую с одним из узлов решетки. Ближайшими к ней будут узлы в позициях А₁, А₂, А₃, отстоящие от О на расстояние . В точке О сходятся ребра восьми соседних ячеек, а так как каждый атом такого рода принадлежит двум смежным ячейкам, то всего на первую координационную сферу попадает  атомов.

Вторая координационная сфера будет иметь радиус, равный а. На нее попадет 6 атомов по трем взаимоперпендикулярным направлениям по осям OX, OY, OZ ( А₄, А₅, А₆).