Методология научного творчества: Учебное пособие, страница 18

Р_i-1, P_i соответствуют определенной последовательности слоев, расположенных от начального к конечному, проведенных через точки  (рис.5). Эти же точки наносят на сетку (рис.6) при решении задачи численным методом.

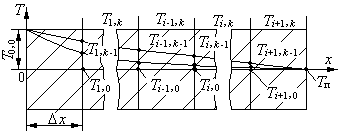
Рис.5. Полуограниченное тело с одномерным температурным полем

  

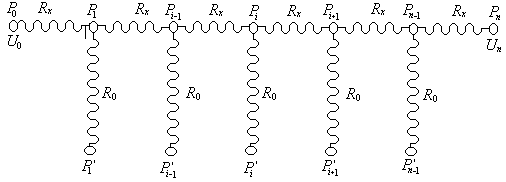
Рис.6. Схема электрического аналога одномерного температурного

поля полуограниченного тела

          К точкам и  подводят напряжения, соответствующие температурам, заданным в краевых условиях. К точке Р₀ подводится напряжение u₀, соответствующее заданной начальной температуре Т₀ начальной поверхности  тела в момент времени , к точке Р_n – напряжение u_n, соответствующее заданным начальной температуре Т₀ в n-ном слое.

          К точкам  – подведены напряжения , соответствующие заданным начальным температурам  в слоях тела, расположенных на расстоянии  от наружной поверхности.

          При этом в узловых точках схемы  наводятся соответствующие напряжения , отражающие величину искомых температур  в слоях тела  в момент времени . Таким образом с использованием метода электротепловой аналогии опытным путем найдены  температуры, которые ранее были нами определены при иллюстрации численных методов решения теплофизических задач.

          Вернемся к модели электротепловой аналогии и рассмотрим какие условия необходимо соблюсти, чтобы явления удовлетворяли условиям аналогии. Как уже отмечалось ранее они должны описываться одинаковыми по форме математическими зависимостями:

          теплопроводность – законом Фурье

;

          электропроводность – законом Ома

,

где  – плотность теплового потока, Вт/м²; l – теплопроводность, Вт/мК; Т – температура, К;  – плотность электрического тока, А/м²; s  – электропроводность, 1/Ом×м; gradu – градиент электропотенциала, В/м.

          Как уже отмечалось, изготовив электрическую модель и создав на ее границах условия, соответствующие реальным граничным условиям, можно, измерив электропотенциал в любой точке, определить по нему температуру в соответственной точке температурного поля.

          Достоверность результатов может быть обеспечена геометрическим подобием, а также граничные условия электрического аналога – модели должны быть подобны температурным (тепловым) граничным условиям электрического анализа. Рассмотрим как добиться этого подобия на простейших примерах.