Методология научного творчества: Учебное пособие, страница 16

                                                       ,                                                      (4)

где Н считается соответствующим по величине потенциалу u в измеряемых точках.

Линии тока обычно строят графически, проводя их по нормали к найденным линиям постоянного напора .

Поперчное сечение гидросооружения

Модель электроаналогии из электропроводящей бумаги

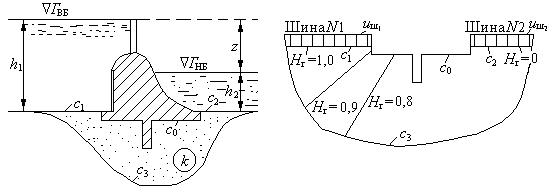
                                                 а                                                                   б

Рис.2. Пример электрогидродинамической аналогии

          Для однородного грунта линии тока можно построить также как линии . В этом случае электрические шины необходимо прикладывать к границам С₀ и С₂ модели и рассматривать схему обратную, представленной ранее, рис.3.

         Самой верхней линией тока  является линия подземного контура гидротехнического сооружения. Этой линии тока приписывается нулевая напряженность .

        Весь расход воды, протекающий под сооружением, выражается наименованием последней линии тока , где q – расход воды, м³/с.

В этом случае линии j и y проводятся в сетке так, что . Линии  и  имеют одинаковую размерность м²/с. В этом случае имеет место квадратичная сетка, клетка которой представляет собой криволинейный квадрат с равенством длин сторон . Такая сетка характеризует две взаимные кинематические схемы – прямую и обратную.

          При использовании метода ЭГДА необходимо различать два разных устройства:

-  модель области фильтрации, выполненную из электропроводного материала;

-  электроприспособление, позволяющее пропускать через модель постоянный электрический ток в нужном направлении и измерять величину электрического потенциала различных точках модели.

          На примере рассмотрен плоский вариант задачи напорной фильтрации в однородной изотропной среде. Однако метод ЭГДА при использовании соответствующего по своим свойствам электропроводящего материала может быть применим для построения гидродинамической сетки и для неоднородной области фильтрации (, где k – коэффициент фильтрации, м/с) и для случая аутотропного грунта. Создавая электропроводные модели пространственного типа можно по этому методу получить решения и пространственных (объемных) задач.

          В качестве другого примера приведем исследование стационарной теплопроводности методом электротепловых аналогий.

          Расчет задач стационарной теплопроводности сводится к интегрированию дифференциального уравнения Лапласа [11]

                                                             .                                                        (5)