Методология научного творчества: Учебное пособие, страница 10

При построении графика следует уделять внимание выбору масштаба независимой и зависимой переменной так, чтобы поле, определяющее функционирование системы, было загружено полностью.

       

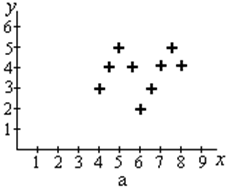
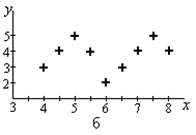
Рис. 1. Примеры неудачного (а) и правильного (б) построения графиков

Так, в представленном на рисунке модельном эксперименте значения задаваемой переменной функционирования системы x начинаются с цифры 4, равно как и значения y – отклики системы на внешнее воздействие x заключены в пределах [2,4].

       Естественно было бы рекомендовать растянуть масштаб по оси x и y, включив в график только поле экспериментальных точек, исключить пробелы, и по возможности увеличить число экспериментальных точек. Более оптимальным было бы другое представление графика.

          В некоторых случаях рекомендуется использовать не простые  (натуральные), а функциональные шкалы.

          Так, например, при экспериментальном исследовании электрической проводимости, полупроводниковой температуры Т ставится задача определения константы  зависимости , где Т – абсолютная температура. Графическое представление зависимости  удобнее выполнить в виде

.

          У исследователя появляется обычно желание провести операцию сглаживания экспериментальных результатов некоторой математической зависимостью. В основе этой процедуры лежит метод наименьших квадратов, предложенный впервые Гауссом.

          Наиболее просто определяются параметры линейной зависимости . Часто встречающийся в экспериментальной практике случай – использование параболической зависимости .

          Теоретически возможно использование и многочленных зависимостей вида , однако определение коэффициентов зависимости может существенно усложнится из-за неустойчивости решений. Поэтому наиболее часто реализуемые случаи – это представление результатов в качестве двух параметрических зависимостей вида : 

,  , ,  , .

          Достаточно популярным у экспериментаторов является сглаживание экспериментальных данных с помощью полиномов Чебышева , где  – полиномы Чебышева,  – коэффициенты, определяемые на основе массива экспериментальных данных.

          Следует иметь в виду, что анализ полученных экспериментальных результатов, не менее ответственная операция, чем сам эксперимент.                                     

3 Основные методы теоретического познания

3.1 Связь конкретных научных исследований с философией

          В основе любого научного процесса лежат философские аспекты. Эта взаимосвязь для исследователя может проявляться подспудно и при проведении конкретного инженерно-физического эксперимента и его теоретического осмысления, она не всегда реализуется в явном виде. Однако философский элемент как правило присутствует при любой ситуации и его влияние усиливается при проведении фундаментальных исследований, имеющих принципиальное значение для основ науки.