Методология научного творчества: Учебное пособие, страница 17

          Интегрирование уравнения (5) при известных граничных условиях позволяет найти совокупность значений температуры Т в каждой точке тела – температурное поле в виде функций . При известной функции   плотность теплового потока рассчитывается по гипотезе Фурье

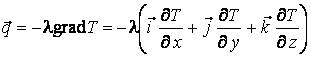                                  ,                               (6)

где l – теплопроводность материала, Вт/мК.

          В случаях, когда аналитическое решение задачи теплопроводности невозможно, а численное решение носит достаточно громоздкий характер, можно использовать метод гидродинамической или электротепловой аналогии.

          Задачи двумерной стационарной теплопроводности могут быть смоделированы безвихревым () потоком идеальной жидкости.

          Запишем дифференциальное уравнение для функции тока потенциального двумерного течения идеальной жидкости

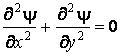                                                                                                          (7)

          Линии тока определяются очевидным уравнением . Гармонически сопряженной с y является функция j, представляющая собой потенциальную функцию скоростей потока. Как было уже отмечено ранее, обе эти функции y и j удовлетворяют уравнению Лапласа (7).

          Функция распределения температуры двумерного температурного поля  имеет вид

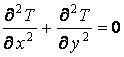                                                                                                          (8)

как видно тоже (8) представляющий собой уравнение Лапласа. Линии тока и эквипотенциальные линии скоростей взаимно перпендикулярны. Таким образом, линии плотности теплового потока и температурного потенциала при стационарной теплопроводности аналогичны соответственно – линиям тока и потенциалу скоростей двумерного потока идеальной жидкости.

Используя различные методы визуализации течений линии тока в жидкости можно сделать видимыми, например, вводя в поток тушь, чернила или кристаллы марганцовокислого камня, которые растворяясь в воде в процессе перемещения оставляют видимые следы – линии тока [3]. Они идентичны линиям постоянного теплового потока. Это позволяет по ним экспериментально установить характер расположения линий  постоянного теплового потока, по которым впоследствии строятся изотермы – линии постоянной температуры, определяющие характер температурное поле (рис.4).

При использовании для решения задач теплопроводности метода электротепловой аналогии исследуемое тело заменяется аналогичной электрической цепью, составленной из определенным образом сочлененных омических сопротивлений. В [2] рассмотрен пример решения задачи нестационарной теплопроводности в полуограниченном теле при одномерном температурном поле с использованием метода электротепловой аналогии.

          Схема полуограниченного тела представлена на рис.5, а на рис.6 приведена схема электрического аналога его температурного поля.

          Начало электрической цепи точка Р₀ соответствует границе исследуемого полуограниченного слева тела – наружной поверхности левого торца. Цепь в точке Р_n соответствует n-ному слою тела, если по условию задачи последнее сечение, в котором требуется найти температуру, имеет номер n-1. Точки Р₁,