При расчете гидротехнических сооружений часто используют гидродинамические сетки. Известно, что между функцией тока и потенциалом скорости существуют следующие соотношения [1].
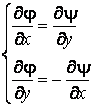(1)
Следует отметить, что функция y так же, как и j,должны удовлетворять уравнению Лапласа
и 
.
Учитывая двухмерность гидротехнических задач, запишем:
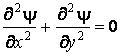и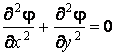 
.
Следовательно
функции y
и j
являются сопряженными гармоническими функциями и по одной из них можно найти
вторую. Вспоминая, что линии 
представляют
собой живые сечения, можно сделать вывод о том, что линии y
и j
образуют ортогональную гидротехническую сетку, которую можно построить, например,
для заданной области фильтрации, решив уравнение Лапласа для этой области. Для
областей сложной конфигурации построения таких сеток решением уравнения Лапласа
представляет собой достаточно сложную расчетную математическую процедуру.
Сложность построения гидродинамических сеток привела к появлению различных
приближенных методов решения задач, без построения сеток.
В 1921-1922 гг. Н.Н. Павловским был предложен экспериментальный метод электрогидродинамических аналогий (метод ЭГДА), позволяющий построить гидродинамическую сетку для области фильтрации сложной формы. Движения воды в грунте в процессе фильтрации и электрических зарядов при токе в проводнике в некоторой степени аналогичны и описываются одинаковыми по форме математическими зависимостями:
,
(2)
u – скорость фильтрации грунтовых вод, м/с; k – коэффициент скорости; H – напор грунтовых вод, Па.
,
(3)
где j – плотность тока, А(м2×с); с – электропроводность; u – электрический потенциал, В.
Очевидно величинам u, k, H в случае движения грунтовых вод в аналогичном процессе протекания электротока будут соответствовать величины j, c, u.
Функция u также как и напор Н должна удовлетворять уравнению Лапласа.
Построение гидродинамической сетки по методу ЭГДА происходит следующим образом. Пример заимствован из источника [10].
Рассмотрим схему гидросооружения, представленного на рис.2,а. Ее электрическая аналогия, выполненная из электропроводящей бумаги.
Рис.2,б отражает характерные особенности геометрии и уровни зеркала водной глади.
Модель
основания (сечения) должна быть геометрически подобна действительному
водонепроницаемому основанию. К электропроводной модели прилагают электрические
шины, которым сообщают соответствующие потенциалы 
и
. Под действием разности потенциалов 
в модели основания возбуждается
постоянный электрический ток. Разность потенциалов принимается равной 
. Линии равного потенциала на модели
нащупывают иглой измеряя потенциал с помощью высокоточного потенциометрического
моста Уитстона.
Полученные
эквипотенциальные линии равного потенциала 
принимают
за линии равного напора 
(за живые сечения
фильтрационного потока). Их численное значение устанавливают по зависимости
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.