Надежность горных машин и оборудования: Методические указания к практическим занятиям по решению задач на определение показателей надежности, страница 9

Установить, что экспериментальные данные не противоречат принятому теоретическому закону распределения, можно с помощью критериев (хи-квадрат) (критерий Пирсона) или критерия Колмогорова. Критерий (хи-квадрат) определяют по формуле

,

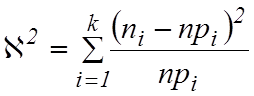где   - число интервалов статистического распределения;  - количество значений случайной величины в каждом интервале;  - теоретическая вероятность попадания случайной величины в -й интервал.

.

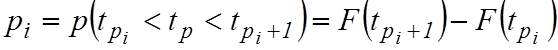Распределение  зависит от числа степеней свободы:

,

где  -число связей, наложенных на частоты, т.е. число параметров распределения, оценки которых вычислены. Для нормального и экспоненциального распределений .

Значения  приведены в табл.12, пользуясь которой, можно для вычисленных значений  и  найти вероятность  того, что величина, распределенная по закону , не превзойдет это значение. Если полученная вероятность больше 0,05-0,1, можно признать, что экспериментальные данные не противоречат принятому теоретическому закону распределения случайной величины.

        Наряду с критерием согласия  используется также критерий А.Н.Колмогорова. В качестве меры расхождения между теоретическим и статистическим распределениями в этом случае рассматривают максимальное значение модуля разности между статистической функцией распределения  и соответствующей теоретической функцией , т.е. 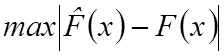, величину которого находят из графиков  и . Далее определяют величину 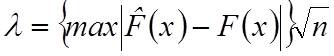 и по табл.13 находят вероятность .

Наиболее часто критерий А.Н.Колмогорова применяют в тех случаях, когда гипотетическое распределение случайной величины известно заранее из каких-либо теоретических предположений.

Пример 1

В результате хронометражных наблюдений получено 205 случайных значений времени безотказной работы  бурового станка, которые приведены в табл.14.

Необходимо определить  оценку наработки на отказ и вид закона распределения случайных значений времени безотказной работы  бурового станка.

                                                                                                                                                  Таблица 12

Значение  в зависимости от  и