Надежность горных машин и оборудования: Методические указания к практическим занятиям по решению задач на определение показателей надежности, страница 3

Среднее время безотказной работы вычислим, предположив, что были испытаны только те валики, которые были разрушены:

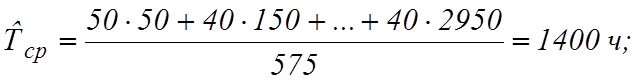
Пример 3

Горная машина имеет наработку на отказ 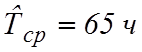 и среднее время восстановления . Необходимо определить коэффициент готовности машины.

Решение

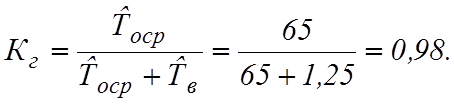
Задачи для самостоятельного решения

1. На стендах поставлено на испытание 100 одинаковых изделий (узлов). За 4000 ч отказало из них 50. За интервал времени 4000-4100 ч отказало еще 20. Определить частоту и интенсивность отказов изделий в промежутке времени 4000-4100 ч, а также вычислить вероятность безотказной работы за время 4000 и 4100 ч.

Ответ:

2. В результате наблюдения за 45 узлами получены данные до первого отказа всех 45 узлов (см.табл.4). Необходимо найти вероятность безотказной работы, частоту отказов, интенсивность отказа и среднюю наработку до отказа.

                                                                                               Таблица 4

Исходные данные к задаче 2

, ч		, ч		, ч
0-10	19	30-40	3	60-70	1
10-20	13	40-50	0
20-30	8	50-60	1

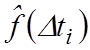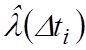Вычисленные значения ;  и  приведены в табл.5,  .

                                                                                                  Таблица 5

Ответы к задаче 2

, ч
0-10	0,577	0,0422	0,054
10-20	0,208	0,0289	0,066
20-30	0,111	0,018	0,089
30-40	0,044	0,007	0,08
40-50	0,044	0	0
50-60	0,022	0,002	0,066
60-70	0	0,002	0,2

3. В течение времени  производилось наблюдение за работой оборудования карьера и было зафиксировано  отказов. До начала наблюдения машины наработали t_1r.  Общее время наработки к концу наблюдений составило t_2r. Требуется найти наработку на отказ. Варианты задачи приведены в табл.6.

    Таблица 6

Варианты исходных данных задачи 3

№ варианта	Исходные данные				Ответ Тср, ч
	t1, ч	t2, ч
1 2 3 4 5 6	350 400 1000 770 1200 300	1280 1600 6400 4800 5558 540		15 3 9 7 2 12	62 400 600 575,7 2179 20

4. Известно, что параметр потока отказов машины выражается формулой 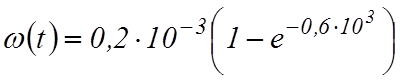. Найти среднюю наработку машины.

Ответ:   .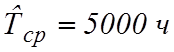

5. Параметр потока отказов сложной восстанавливаемой системы равен 0,0151 ч. Среднее время восстановления . Вычислить вероятность нахождения системы в исправном состоянии.

Ответ:  К_Г=0,398.

ЗАНЯТИЕ 2

Определение показателей надежности при известных законах их распределения

Основные сведения о законах распределения случайных

величин

Закон распределения времени работы изделия (машины) до отказа, выраженный в виде плотности вероятности f(t) или в виде функции распределения F(t), является полной характеристикой его надежности. Фактически математическое описание (принятый закон распределения), которым представляется (аппроксимируется) истинное распределение, является лишь его теоретической моделью.

Основная задача теории надежности состоит в выявлении и математическом описании истинного закона распределения с возможно большей степенью достоверности.

При изучении надежности горных машин и комплексов наиболее часто применяют законы распределения: нормальный (Гаусса), логарифмически нормальный, экспоненциальный, Вейбула и Релея.

Нормальный закон распределения рекомендуется применять при постепенных отказах.

Логарифмически нормальный закон целесообразно применять при обработке данных об ускоренных испытаниях в условиях форсированной нагрузки.