Геология \ Надежность горных машин и оборудования

Надежность горных машин и оборудования: Методические указания к практическим занятиям по решению задач на определение показателей надежности, страница 6

Индекс плана

Описание плана

[N, M(r,TS)]

План испытаний, согласно которому испытаниям подлежит N объектов; после каждого отказа работоспособность объекта восстанавливается; каждый объект испытывается до возникновения  r отказов, либо до суммарной наработки TS всех объектов в зависимости от того, какое из этих условий будет выполнено раньше

[N, M, rS]

План испытаний, согласно которому испытаниям подлежит N объектов; после каждого отказа работоспособность объекта восстанавливается; испытания прекращаются при возникновении суммарного числа rS отказов с учетом всех объектов

[N, M, TS]

План испытаний, согласно которому испытаниям подлежит N объектов; после каждого отказа работоспособность объекта восстанавливается; при получении TS суммарной наработки всех объектов испытания прекращаются

Число объектов наблюдений (испытаний) зависит от вида закона распределения и может определяться по формулам табл.9.

                                                                                                 Таблица 9

Формулы для определения числа испытываемых объектов

Закон распределения

Формула для определения N

Нормальное распределение

Распределение Вейбула

Логарифмически нормаль-

ный закон распределения

В табл. 9   - число отказов;  n- коэффициент вариации;  - нормированная функция Лапласа; - гамма- функция;  - относительная продолжительность испытаний; - коэффициент распределения Вейбула.

Для экспоненциального распределения формулы для определения точечных оценок интенсивности отказов  приведены в табл.10.

    Таблица 10

Формулы для определения точечных оценок

Планы

испытаний

[NUN]

[NUT]

[NUr]

[NRT]

[NRr]

Здесь   - число испытываемых изделий; - число отказов за время Т;

Т – установленная продолжительность наблюдений (испытаний);  - число отказов, до которого проводятся испытания;  - наработка изделия до получения r отказов.

Экспоненциальное распределение имеет параметр , связанный с наработкой на отказ То соотношением .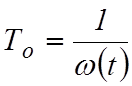

Для планов [NMT] и [NMTS] 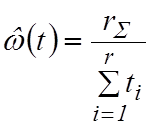, а для планов [NMr]  и [NMrS] 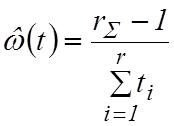, где - суммарное число отказов машин; 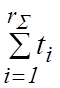- наработка машин за время наблюдений.

Типовые примеры и их решение

Пример 1

При наблюдении за работой экскаваторов по плану [NMr],  где

N = 3  и  r = 5,  наработки  составили    и . Найти оценку параметра потока отказов, если закон распределения экспоненциальный.

Решение

Общее число отказов .

Общее время наблюдений .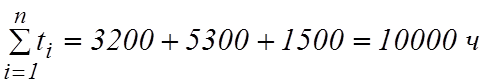

При плане [NMr]  .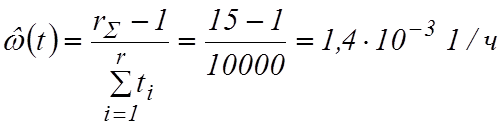

Пример 2

При испытаниях 20 пружин по плану [NRT] число отказов за время испытаний в течение 100 часов составило 7. Найти оценку интенсивности отказов, если закон распределения экспоненциальный.

Решение

Для экспоненциального закона распределения

.

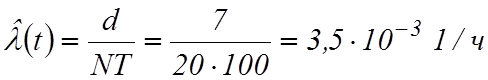Задачи для самостоятельного решения

Задача 1

При наблюдении за работой подъемных лебедок трех экскаваторов-мехлопат по плану [NМT] наработка лебедок составила 2300 ч, при этом первая лебедка отказала 1 раз, вторая 2 раза, а третья работала безотказно. Найти оценку параметра потока отказов, если закон распределения экспоненциальный.

                                                                   Ответ: .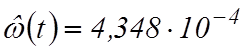

Задача 2

При наблюдении за работой роторного комплекса по плану [NMrS] было зафиксировано 60 отказов в течение 444 ч. Закон распределения экспоненциальный. Найти оценку параметра потока отказов.

Ответ: .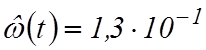

Задача 3

Результаты наблюдений за работой 23 буровых станков приведены в табл.11.

                                                                                              Таблица 11

Результаты наблюдений

Скачать файл