Надежность горных машин и оборудования: Методические указания к практическим занятиям по решению задач на определение показателей надежности, страница 4

Экспоненциальный закон является моделью распределения внезапных отказов, характерных для периода нормальной работы машины и ее неремонтируемых элементов.

Закону распределения Вейбула подчиняются усталостная прочность подшипников качения и зубчатых колес, пределы выносливости некоторых материалов. При этом при в=1 закон Вейбула превращается в экспоненциальный, а при в<1 он близок к нормальному. При в=2 получается распределение Релея.

В табл.7 приведены аналитические выражения для количественных показателей надежности при различных законах распределения.

Таблица  7

                                        Показатели надежности при различных законах распределения

Закон распреде-ления

Вероятность отказа               f(t)

Вероятность безотказной работы р(t)

Интенсивность отказов l

Наработка на отказ                    Тср

Экспоненциальный
Релея
Вейбула

             Продолжение табл. 7

Закон распреде-ления	Вероятность отказа               f(t)	Вероятность безотказной работы р(t)	Интенсивность отказов l	Наработка на отказ                    Тср
Усеченный нормальный
Логарифмически нормальный

В формулах табл.7 приняты обозначения:

-интеграл вероятностей или нормированная функция Лапласа. Её значения приведены в прил. 1;

t - время работы (наблюдения); а- параметр масштаба; в- параметр формы; - среднеквадратическое отклонение времени безотказной работы; Г- гамма-функция. Её значения приведены в прил. 2; r(t)- число отказов за время t; р(t)- вероятность безотказной работы за время t; f(t)- частота отказов за время t; l(t)- интенсивность отказов; w(t)- параметр потока отказов; Тср- средняя наработка на отказ; КГ - коэффициент готовности.

Типовые примеры и их решение

Пример 1

Структура комплексной механизации состоит из пяти горных машин, работающих последовательно.

Известно, что первая машина отказывала 34 раза в течение 952 ч работы, вторая 24 раза в течение 960 ч работы. Остальные в течение

210 ч отказали 4, 6 и 5 раз, соответственно.

Требуется определить наработку на отказ всей структуры, если справедлив экспоненциальный закон надежности для каждой горной машины.

Решение

Поскольку   r₁=34;     r₂=24;    r₃=4;    r₄=5;      r₅=6;

t₁=952 ч;      t₂=960 ч;        t₃= t₄= t₅=210 ч,

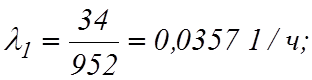
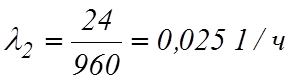              и

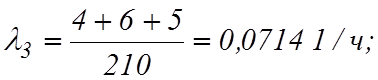
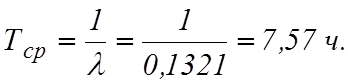
Пример 2

Время работы драглайна до отказа подчинено экспоненциальному закону распределения с 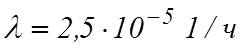. Вычислить ;  и , если время работы t = 500ч, 1000 ч и 2000 ч.

Решение

Вероятность безотказной работы ;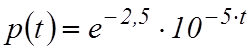

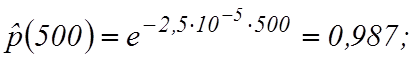
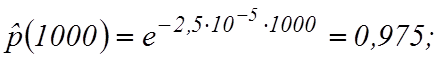
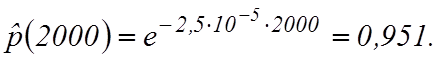
Частота отказов  или ;

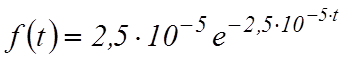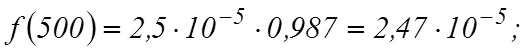
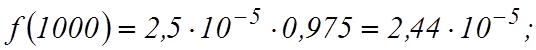
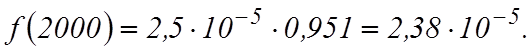
Наработка на отказ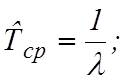

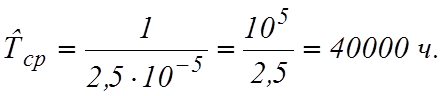
Пример 3

Время работы мехлопаты подчинено усеченному нормальному закону с параметрами   и   Вычислить , ,   и Т для  t = 4000; 6000; 8000 и 1000 ч.

Решение

Вероятность безотказной работы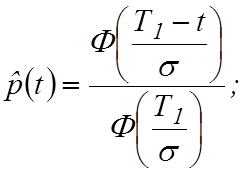

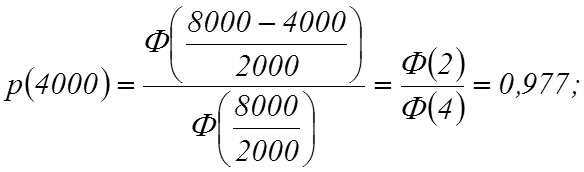
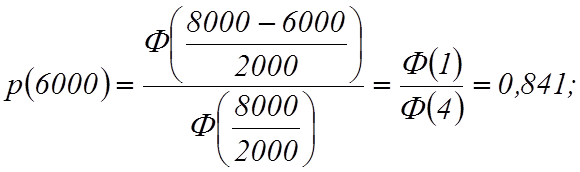
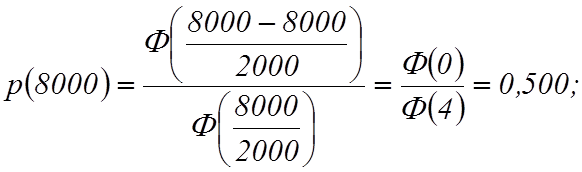
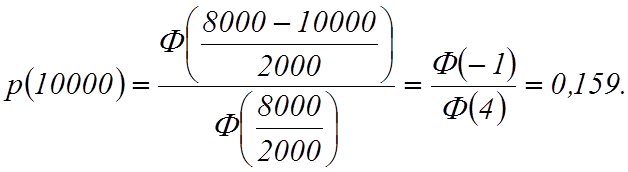
Определим частоту отказов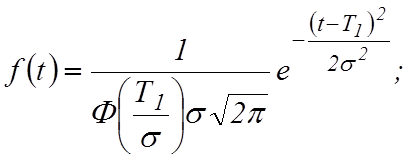 

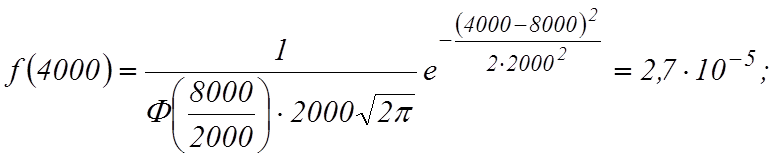
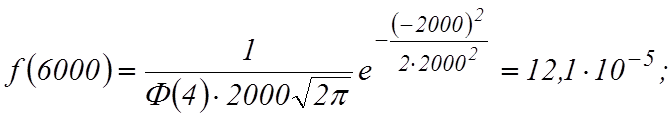
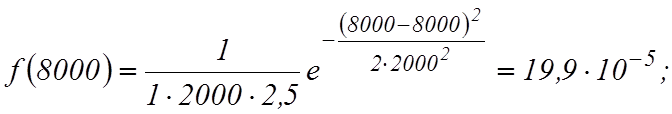
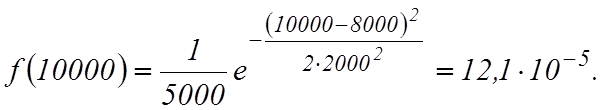
Определим интенсивность отказов, имея в виду, что

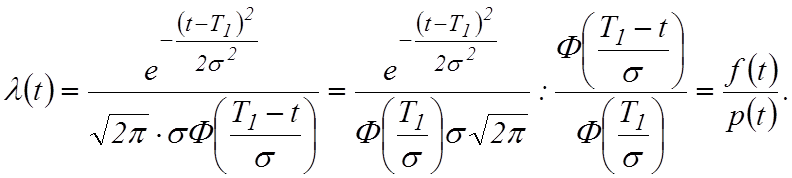
Используя вычисленные значения  и , получим

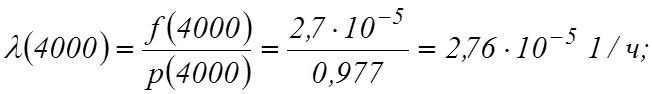
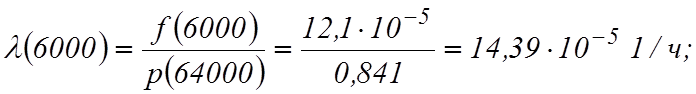
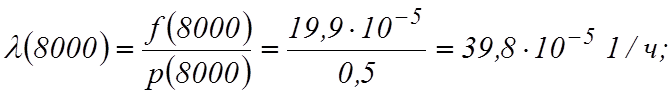
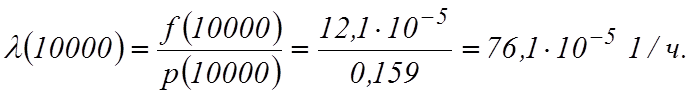
Вычислим среднюю наработку до отказа:

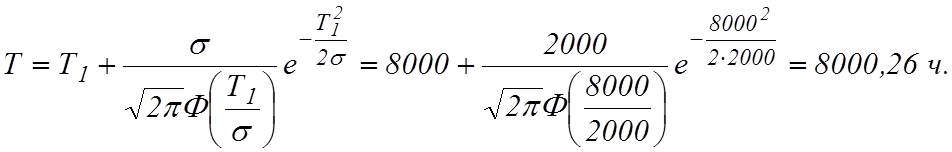
Пример 4

Время безотказной работы конвейерной ленты роторного комплекса подчиняется закону Вейбула с параметрами 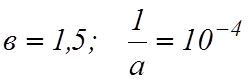, а время ее работы .

Требуется вычислить количественные показатели надежности ленты  и .

Решение

Вероятность безотказной работы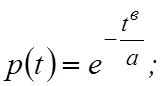 

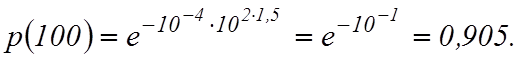
Интенсивность отказов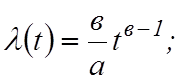

.

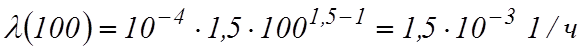Средняя наработка до отказа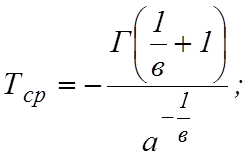

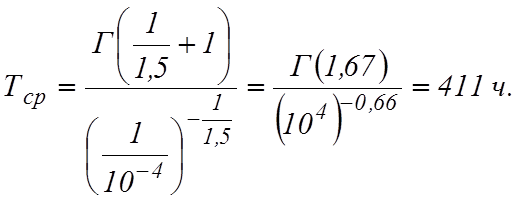
Пример 5

Известно, что интенсивность отказов ленточного конвейера , а среднее время восстанавливания . Вычислить коэффициент готовности К_Г  и функцию готовности при экспоненциальном законе распределения времени до отказа.

Решение

Наработка до отказа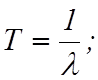   

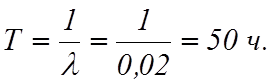
Коэффициент готовности