Надежность горных машин и оборудования: Методические указания к практическим занятиям по решению задач на определение показателей надежности, страница 13

Поскольку при экспоненциальном законе 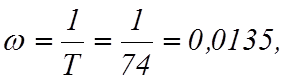 то выравнивающая кривая .

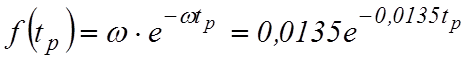Находим критерий , для чего вычислим предварительно

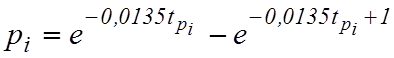. Результаты вычислений приведены в табл.17.

                                                                                                      Таблица 17

Результаты вычислений

10	0,1262	110	0,1131
20	0,1104	150	0,0943
30	0,0964	190	0,0551
50	0,1579	250	0,0427
80	0,1795	370	0,0278

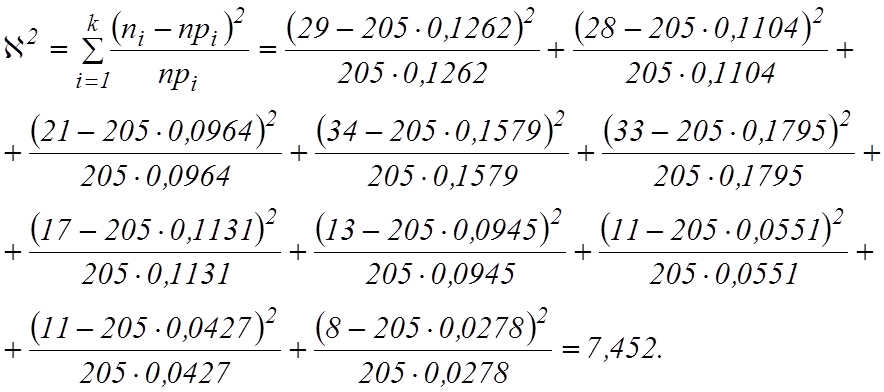
Для экспоненциального закона число связей  и число степеней свободы  По табл.12 для   и  Полученная вероятность  не является малой, поэтому гипотезу распределения  по экспоненциальному закону можно считать правдоподобной.

Пример 2

Интервалы статистического ряда 210 случайных значений времени восстановления  комбайна 1К-52Ш и результаты расчетов приведены в табл.18.

                    Таблица 18

Статистический ряд и результаты расчетов

Интервалы
0-5	50	0,238	0,238	0,0476
5-10	57	0,271	0,509	0,0542
10-15	41,5	0,198	0,707	0,0396
15-20	15,5	0,074	0,781	0,0148
20-30	18	0,086	0,867	0,0086
30-40	12	0,057	0,924	0,0057
40-120	16	0,076	1,000	0,00095

Необходимо найти закон распределения случайных значений времени восстановления  и выравнивающую кривую .

Решение

1. Находим оценки математического ожидания, дисперсии и среднего квадратического отклонения:

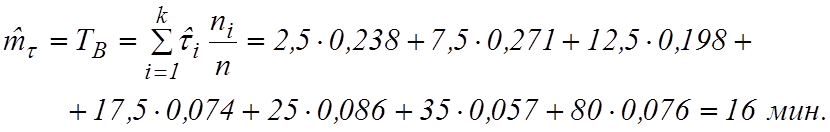
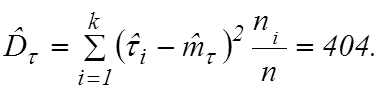
Среднее квадратическое отклонение

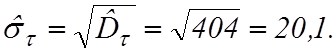
Существенное расхождение по величине оценок математического ожидания и среднего квадратического отклонения не позволяет принять гипотезу об экспоненциальном законе распределения случайных значений времени восстановления.

2. По данным табл.7 строим гистограмму (рис.2, прил.5). Из характера гистограммы можно предположить, что случайные значения  имеют логарифмически-нормальное распределение.

Для построения выравнивающей экспериментальное распределение кривой логарифмически-нормального распределения необходимо найти параметры распределения: 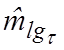- оценку математического ожидания логарифма случайной величины    -  оценку среднего квадратического отклонения  .

Кривая плотности распределения

.

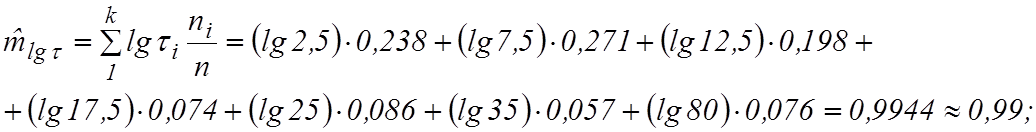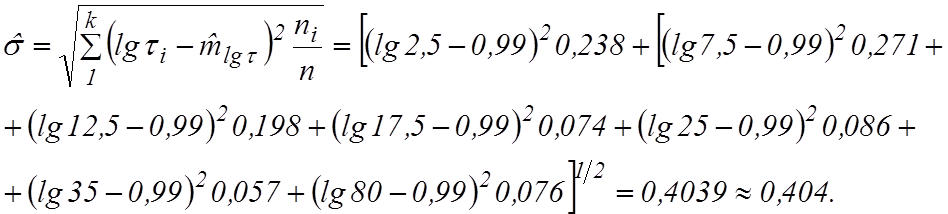
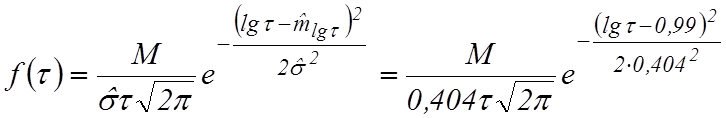Задачи для самостоятельного решения

Задача 1

На рис.3 прил.5 приведены графики статистической  и теоретической  функций распределения для рассмотренного в разд. 2 примера 1.

Проверить, пользуясь изложенной выше методикой и критерием Колмогорова, подтверждается ли гипотеза об экспоненциальном законе распределения времени безотказной работы .

Ответ: подтверждается, т.к.

Задача 2

Найти оценку наработки на отказ и вид закона распределения случайных значений времени безотказной работы  узла горной машины, результаты наблюдений за работой которого приведены в табл.19.

                          Таблица 19

Результаты наблюдений за работой узла горной машины

№ реализации	, ч	№ реализации	, ч	№ реализации	, ч
1	0,8	8	3,6	15	11,6
2	1,5	9	3,9	16	14,1
3	1,7	10	5,7	17	17,0
4	1,9	11	7,9	18	20,8
5	2,0	12	9,6	19	20,2
6	2,1	13	10,4	20	38,6
7	2,3	14	10,6	21	45,8