Пример 2
Требуется определить условия испытаний партии
неремонтируемых изделий 
штук при 
и
сформулировать условия приемки.
Решение
1.
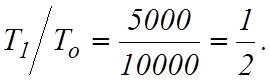
2.
По таблице прил.3 для 
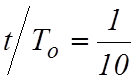находим, что при 
и
.
3.
Находим 
.
Партия объемом 170 изделий полностью испытывается в течение 1000 ч. Если до этого времени откажет 23 изделия, испытания прекращают, и партию не принимают. Если же по истечении 1000 ч отказавших изделий будет меньше 23, партию принимают.
Пример 3
Испытывается партия изделий с заменой отказавших в
процессе испытаний. Заданы значения величин риска 
и
. Время испытаний 500 ч, 
и 
.
Решение
1.
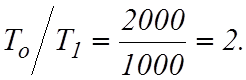
2.
По таблице прил.4 для и устанавливают,
что ближайшим к отношению 
является 
.
3.
Определяем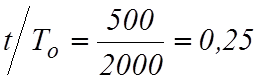 
.
4.
По таблице прил.4 для определяют предельное число отказов 
и 
.
5. Объем выборки (количество испытываемых изделий):
.
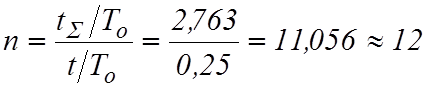Если за время 
произойдет
не более трех отказов, партию принимают.
Задачи для самостоятельного решения
Задача 1
Определить предельное число отказов (
) и количество изделий, которые нужно
поставить на испытания (n) для партии изделий, испытываемых без замены
отказавших, с приемочным уровнем наработки на отказ и
браковочным уровнем 
при величинах риска
поставщика и потребителя 
.
Ответ: 
.
Задача 2
Определить предельное число отказов () и время t
испытаний (без замены отказавших изделий) для партии в 100 шт. При , 
,
и 
.
Ответ: 
.
Задача 3
Определить и число
испытываемых изделий n от партии, если время испытаний 600 ч, 
, 
,
и 
.
Испытания проводятся с заменой отказавших изделий.
Ответ: 
.
ЗАНЯТИЕ 5
Обработка статистической информации о надежности
Основные сведения и теоретические предпосылки
Статистическая функция распределения и величины показателей надежности, определяемых на основании ограниченного объема данных, содержит элементы случайности. Вследствие этого значения параметров можно получить лишь с некоторой вероятностью, и такие параметры называются «оценками». Оценкой функции распределения и является статистическая функция распределения.
Статистический материал, полученный в результате наблюдений или эксперимента, целесообразно представить в виде статистического ряда.
Для этого весь диапазон полученных n
значений случайной величины разбивают на интервалы. Интервалы целесообразно
принимать равными. Их количество при 
определяют по
формуле
.
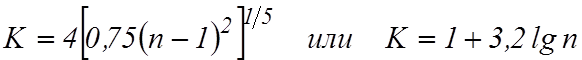При малых n (
) принимают
.
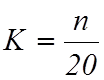Если при равных интервалах количество значений в интервале оказывается
меньше 5-10, принимают интервалы различной длины. Для каждого интервала
подсчитывают: 
- количество значений
случайной величины, попавших в интервал; 
-
частота;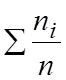 
- накопленная частота; 
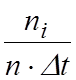- эмпирическая плотность
вероятности.
Суммарная накопленная частота для всех интервалов должна быть равна единице.
В случае попадания значения случайной величины на границу интервалов
значения в смежных интервалах увеличиваются
на 1/2.
Далее находят статистическое среднее 
и
статистическую дисперсию 
:
,
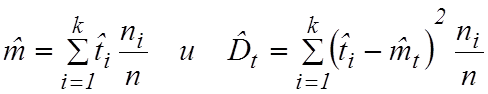где 
- середина i-го
интервала; 
- число интервалов.
По вычисленным значениям эмпирической плотности
вероятност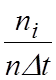и 
и 
строят
гистограмму. Для этого по оси абсцисс откладывают интервалы, и на каждом из них
строят прямоугольник с высотой .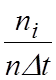
По гистограмме можно предположительно судить о законе распределения случайной величины.
При этом могут быть использованы и некоторые другие
признаки. Например, равенство статистического среднего и
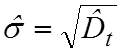свидетельствует о распределении по
экспоненциальному закону.
Приняв предположительно тот или иной закон
распределения, по известным формулам вычисляют его параметры и, рассчитав
значения плотности вероятности 
на границах
интервалов, строят выравнивающую кривую распределения.
При подборе теоретической кривой между нею и статистическим распределением неизбежны некоторые расхождения.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.