|
|
|||||||||||||
|
1 |
7 |
11 |
17 |
21 |
28 |
35 |
44 |
56 |
70 |
92 |
128 |
176 |
248 |
|
2 |
7 |
11 |
17 |
21 |
28 |
36 |
46 |
56 |
70 |
95 |
133 |
180 |
249 |
|
3 |
7 |
12 |
17 |
21 |
29 |
37 |
46 |
59 |
75 |
98 |
135 |
184 |
294 |
|
4 |
8 |
12 |
18 |
21 |
29 |
38 |
47 |
59 |
75 |
100 |
138 |
187 |
314 |
|
4 |
8 |
12 |
18 |
21 |
31 |
38 |
48 |
60 |
76 |
101 |
143 |
188 |
344 |
|
4 |
8 |
14 |
18 |
22 |
31 |
39 |
49 |
60 |
77 |
104 |
144 |
189 |
344 |
|
5 |
8 |
14 |
18 |
22 |
32 |
40 |
49 |
60 |
77 |
105 |
145 |
194 |
362 |
|
5 |
8 |
15 |
18 |
25 |
32 |
40 |
51 |
61 |
78 |
106 |
146 |
206 |
367 |
|
5 |
8 |
15 |
18 |
25 |
34 |
41 |
52 |
62 |
79 |
107 |
148 |
209 |
368 |
|
6 |
9 |
15 |
18 |
25 |
34 |
41 |
53 |
62 |
79 |
107 |
149 |
216 |
370 |
|
6 |
9 |
15 |
18 |
26 |
34 |
42 |
54 |
63 |
82 |
108 |
154 |
224 |
|
|
6 |
9 |
16 |
18 |
26 |
34 |
42 |
54 |
63 |
84 |
109 |
161 |
225 |
|
|
6 |
9 |
16 |
19 |
27 |
34 |
43 |
54 |
64 |
85 |
119 |
165 |
228 |
|
|
6 |
9 |
16 |
21 |
27 |
35 |
43 |
55 |
68 |
87 |
110 |
157 |
237 |
|
|
7 |
9 |
16 |
21 |
27 |
35 |
43 |
55 |
70 |
89 |
125 |
169 |
238 |
|
3. Результаты расчетов для рассматриваемого примера
при разбивке диапазона ![]() на 10 интервалов различной
длины представлены в табл.16.
на 10 интервалов различной
длины представлены в табл.16.
4. Далее находим статистическое среднее 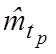 и статистическую дисперсию
и статистическую дисперсию 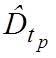 для
для ![]() интервалов:
интервалов:
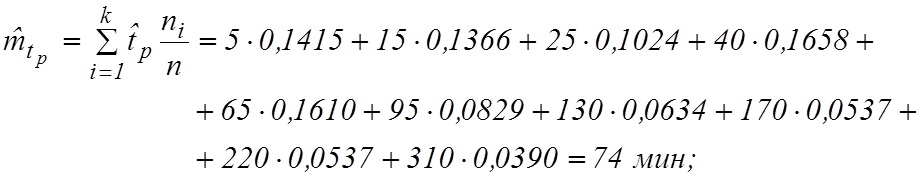
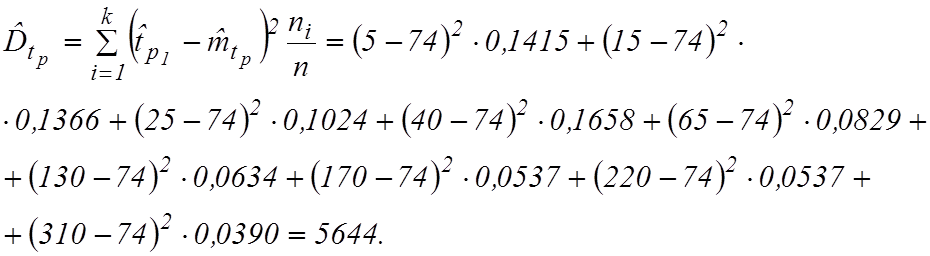
Таблица 16
Результаты расчетов
|
Интервалы
|
|
|
|
|
|
0-10 |
29 |
0,1415 |
0,1415 |
0,01415 |
|
10-20 |
28 |
0,1366 |
0,2781 |
0,01366 |
|
20-30 |
21 |
0,1024 |
0,3805 |
0,01024 |
|
30-50 |
34 |
0,1658 |
0,5463 |
0,00829 |
|
50-80 |
33 |
0,1610 |
0,7073 |
0,00537 |
|
80-110 |
17 |
0,0829 |
0,7902 |
0,00276 |
|
110-150 |
13 |
0,0634 |
0,8356 |
0,00159 |
|
150-190 |
11 |
0,0537 |
0,9073 |
0,00134 |
|
190-250 |
11 |
0,0537 |
0,9610 |
0,00097 |
|
250-370 |
8 |
0,0390 |
1,0000 |
0,00032 |
По данным табл.16 строим гистограмму, представленную на рис.1 (см.прил.5).
Из характера гистограммы можно предположить, что ![]() распределено по экспоненциальному
закону. Об этом свидетельствует также совпадение
распределено по экспоненциальному
закону. Об этом свидетельствует также совпадение 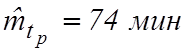 и
и
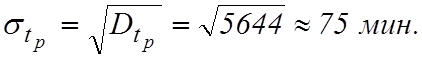
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.