Навигационные параметры и изолинии. Аналитический метод определения места судна с помощью изолиний. Линеаризация навигационных функций и ее геометрическая интерпретация. Априорная и апостериорная оценка точности обсервации

1  Теоретическая часть.

1.1  Навигационные параметры и изолинии

1.1.1  Основные понятия

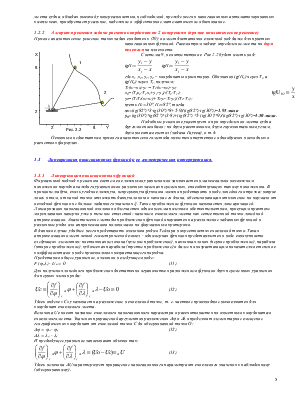
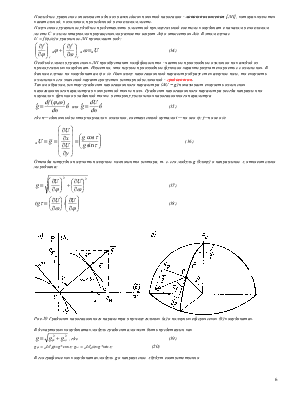
Применяемые системы координат.

В теории МОС принята так называемая левая система координат: ось X направлена по меридиану, а ось Y – по параллели.

Применяется три основных системы координат:

-  географическая система координат ( широта - j, долгота - l) ;

-  прямоугольная локальная система координат с началом в счислимой точке (разность широт - Dj и отшествие - w)

-  сферическая полярная система координат ( сферический угол – y и сферический радиус -r).

Между прямоугольной локальной системой координат и географической существует соответствие:

j = j_с + Dj

l = l_с + w*secj_ср

Одной из основных операций процесса судовождения является определение места судна, основанное на использовании инструментальных измерений различных физических величин. Необходимость такой операции, которую называют обсервацией, обусловлена накоплением погрешностей счисления пути судна. Счисление ведется по лагу и компасу. Полученная в результате такого определения точка называется обсервованной.

Для целей обсервации могут использоваться только те величины, которые функционально связаны с координатами судна и координатами навигационных ориентиров (маяки, навигационные спутники, наземные станции радио - навигационных систем и т.п.)

Линейные и угловые величины, которые зависят от координат навигационных ориентиров и координат судна, называются навигационными параметрами (НП).

Наиболее распространенными НП являются:

- пеленг ориентира,

- расстояние до ориентира,

- горизонтальный угол между двумя ориентирами,

- вертикальный угол удаленного предмета,

- разность расстояний от судна до двух ориентиров,

- угловая высота светила и т.д.

Навигационные параметры на поверхности Земли образуют скалярные поля. А так как координаты ориентиров известны, то множество навигационных параметров зависит только от координат судна.

Функция, связывающая навигационный параметр U с географическими координатами произвольной точки и координатами ориентира называется навигационной функцией. В общем виде в различных системах координат она имеет вид:

U = f(j, l),

U = f(j,w),

U = f(x, y),

гдеj, l,w -географическая широта, долгота и отшествие; x, y -  оси прямоугольной системы координат.

Если зафиксировать некоторое постоянное значение U = U_o, получим уравнение навигационной изолинии, которое в любой систем координат принимает следующий вид:

U_o=f(j, l)=const

U_o=f(j,w)=const

U_o=f(x, y)=const

Навигационной изолинией называется геометрическое место точек равных навигационных параметров.

В качестве примера рассмотрим некоторые из навигационных изолиний.

1.1.2  Изолинии навигационных параметров

Изолиния пеленга на плоскости. При пеленгова­нии на небольших расстояниях (не более 20 миль) допустимо не учитывать кривизну поверхности Земли. Пеленг П с судна остается постоянным в том случае, если судно будет перемещаться по линии, называемой лини­ей пеленга. В прямоугольных относительных и географических координатах уравнение этой изолинии записывается, как уравнение прямой следующим образом:

П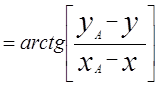                                                                               (1)

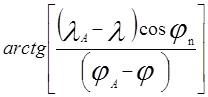П=,                           (2)

где П - пеленг с судна на ориентир А,

j_А, l_А - координаты ориентира,

j, l- текущие координаты места судна,

j_n - промежуточная широта, которая принимается равной средней широте 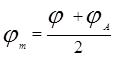 между судном и ориентиром при малых расстояниях.

При пеленговании судна с ориентира в уравнении изолинии следует соответствующим образом изменять знаки Dj и Dw или менять местами географические координаты ориентира и судна.

Изолиния расстояния между судном и ориентиром на плос­кости .Если с судна С измерено расстояние D до ориентира А (рис.1.2),то судно находится на линии равных расстояний от ориентира, которая в навигации называется изостадией.

Общее уравнение изостадии в соответствии с (1.2): U_o=f(j, l)=D=const,

В прямоугольной системе координат это выражение будет иметь вид:

                                                     (4)

Изолиния вертикального угла. В точке С измерен вертикальный угол р между вершиной А и основанием В отдаленного предмета высотой Н. Требование изолинии b-const будет соблюдаться только тогда, когда точка С перемещается в положения Ci...Cn по окружности радиуса R, лежащей в плоскости горизонта. Следовательно, уравнение изолинии вертикаль­ного угла будет иметь вид:

R=H*ctgb = Ö(Dj)² + (Dw)² = Ö(j-j_B)²+(l-l_d)²*cos²j_т

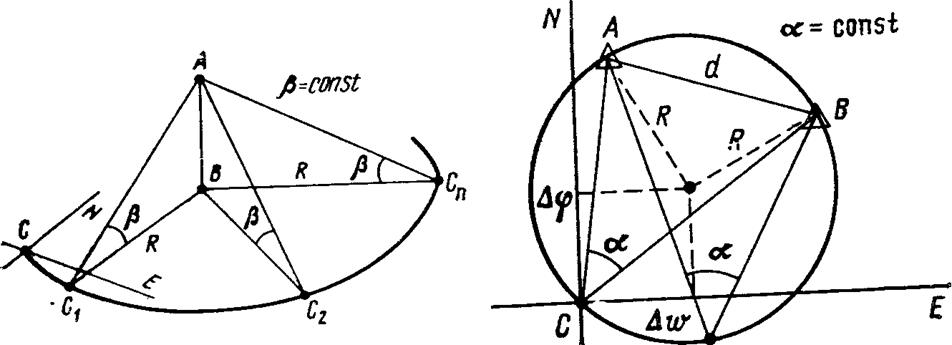
Рис.1 Изолиния вертикального угла                        Рис.2 Плоская изогона

Изолиния   горизонтального  угла  между ориентирами. Вершины постоянного горизонтального угла образу­ют геометрическое место точек окружности, на которую опи­рается этот угол. Уравнение такой окружности связывает пря­моугольные координаты центра окружности относительно точки С, угол a и расстояние между ориентирами:

R == d/2sina =           (5)

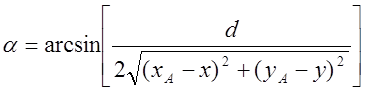                                                       (6)

Изолинию горизонтального  угла часто называют изогоной. Если изолиния определяется на сфере, то ее называют сфери­ческой изогоной.

Изолиния пеленга с судна на ориентир на сфере. С учетом сферичности Земли в навигации определяется радио­пеленг. Для того чтобы величина радиопеленга оставалась по­стоянной, судно должно находиться на кривой Ci-..Сп, пред­ставляющей геометрическое место вершин одинаковых по величине сферических углов П. Уравнение изолинии С₁, Сi,..., Сп на сфере определится по формуле четырех рядом лежащих элементов и после преобразования будет выглядеть как:

Ctg П = tg j_A*cosj*cosec(l_A-l) – sinj*ctg(l_A-l)                 (7)

Такое пеленгование называют обратной радиозасечкой, а полученную при этом изолинию — изопеленгой или изоазимутой.

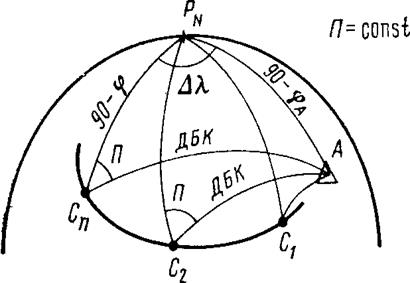
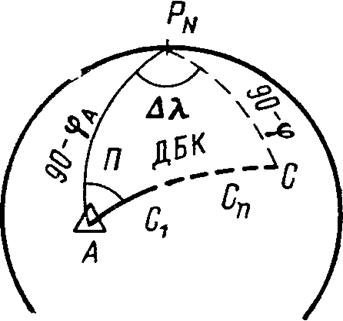
Рис.3 Сферическая изоазимута (изопеленга)                       Рис.4 Ортодромия.

Изолиния пеленга с ориентира на судно на сфере. Если пеленг берется с ориентира на судно (в навигации есть и такие случаи), то изолиния имеет на сферической поверхности форму кривой, соединяющей точку ориентира с судном по крат­чайшему расстоянию. Следовательно, изолинией такого пеленга будет дуга большого круга (ортодромия) Cn-.CiA. Уравнение ортодромии получим, как и в предыдущем случае, с использо­ванием формулы четырех рядом лежащих элементов. В конеч­ном виде это уравнение удобно представить таким образом:

tgj = ctgП*secj_А*sin(l-l_A)+ tgj*cos(l-l_A)                          (8)

Подставляя значения ортодромического пеленга П, коорди­нат ориентира j_А, l_Аи задаваясь величиной долготы судна К. (с шагом 5+10°), можно вычислить широты точек ортодромии и построить ее на морской карте или специальном планшете.

Изолиния расстояния на сфере. На поверхности сферы такая изолиния будет, как и на плоскости, окружностью, но только сферической. Уравнение сферической окружности можно получить по теореме косинуса стороны сферического треугольника СРNА. с использованием формул приведения

cos D = sinj_A*sinj + cosj_A*cos j*cos (l_A-l)                        (9)