Для определения места судна используют прокладку линий положения.
Уравнение линий положения в этом методе записывается так:
aDj + bDw = Du, но можно записать и следующим образом
g cost + g costDw = Du
После нормирования (деления на модуль g)получим
cost + costDw = Du/g = Dn
Dn – смещение (перенос) линий положения.
Аналитическое решение обычно лежит в основе алгоритмов определения места по двум ЛП на штурманских калькуляторах и простейших персональных компьютерах.
Графоаналитическое решение заключается в следующем:
- измерить навигационные параметры Uоi
- найти счислимые значения Uс1 и Uc2, этих же навигационных параметров по счислимым координатам jс и lс на момент измерений;
- вычислить приращения навигационных параметров DUi;
- определить модули градиентов gi и их направления tI;
- рассчитать переносы Dni линий положения для каждой пары измеренных и счислимых навигационных параметров по формуле Dni = Dui/gi;
- на карте или на специальном планшете от счислимой точки С, считаемой началом координат, выполнить прокладку по элементам линий положения Dni τi. Прокладка выполняется следующим образом: в прямоугольных координатах по наибольшей величине переноса выбирается масштаб изображения в милях или кабельтовых (если прокладка ведется не на карте), под углом tι от меридиана откладывается отрезок , равный в выбранном масштабе или масштабе карты переносу Dn1; под углом tI+1 строится перенос Dni+1.
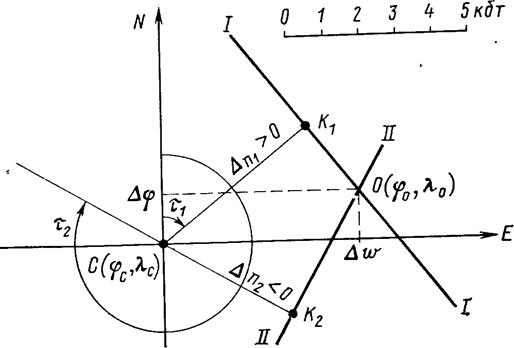
Рис. 20. Прокладка графоаналитического решения задачи определения места судна
Если перенос имеет отрицательный знак, то отрезки подует откладывать в сторону, обратную направлению t. Через определяющие точки К1 и Кг перпендикулярно переносам проводят линии положения до их пересечения в обсервованной точке О. Линии положения обозначают римскими цифрами I-I, II-II;
- если необходимо, снять с прокладки элементарные приращения координат Dj и Dl и рассчитать географические координаты обсервованного места: jо = jс+Dj; lо = lс+Dw secjт.
Решения такого типа обычно применяют в мореходной астрономии и специальных задачах навигации.
Обобщенный метод линий положения некритичен к погрешностям задания счислимого места.
В этом методе итерационная процедура обычно не выполняется.
При графоаналитическом решении определяются только координаты места судна и считают, что систематические погрешности отсутствуют.
Мы можем найти вес каждой точки пересечения линий положения.
p=1/m2
СКП измерений равно:
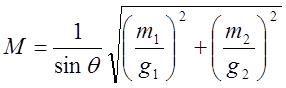 ,
где (101)
,
где (101)
g = 1/D – градиент,
D – дистанция до точки пересечения,
q - острый угол между линиями положения.
Вес каждой точки будет:
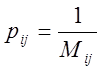 (102)
(102)
Так как точность каждой точки оценивается СКП Mij, то можно найти центр тяжести всей фигуры погрешностей, т.е. рассчитать весовое среднее для Dx и Dy.
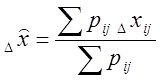 (103)
(103)
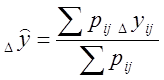
Обсервованные координаты:
xo = xc + Dx
yo = yc + Dy
Транспонирование – операция замены строк соответствующими столбцами
Следом матрицы называется сумма ее диагональных элементов
TR(A) = åaii
Определитель матрицы получается вычеркиванием первой строки и i-того столбца
Det(A) = a11C11+a12C12+…+a1nC1n
Алгебраическое дополнение – умноженный на (-1)j+I определитель матрицы.
Элементами взаимной матрицы С являются алгебраические дополнения I-х, j-х элементов матрицы А
A-1 = (1/det(A))*CT при det(A)¹0
Случайным событием (явлением) называют такое, которое при определенных условиях может либо произойти, либо не произойти.
Вероятностью (P) случайного события называют объективную возможность его появления при определенных условиях. Для достоверных событий вероятность равна 1, для невозможных – 0.
Несовместными называют события, которые никак не могут произойти одновременно.
Случайной величиной называют такую величину, которая может принимать то или иное значение, но не известно заранее, какое именно.
Дискретной называют случайную величину, возможные значения которой могут быть перечислены.
Непрерывной называют случайную величину, возможные значения которой сплошь заполняют некоторый числовой промежуток и составляют несчетное множество.
Закон распределения случайной величины выражает зависимость между всеми ее возможными значениями и вероятностями этих значений.
Ряд распределения применим к дискретным случайным величинам, когда для такой величины перечисляют все возможные ее значения и указывают соответствующие им вероятности.
Функция распределения применима для выражения закона распределения как дискретных, так и непрерывных случайных величин. При любом значении аргумента x эта функция равна вероятности того, что случайная величина X принимает значения, не превышающие x.
Математическое ожидание характеризует среднее значение случайной величины, ее центр, около которого группируются все возможные ее значения.
Дисперсия обобщенно характеризует рассеивание возможных значений случайной величины относительно ее математического ожидания.
Среднее квадратическое отклонение равно положительному квадратному корню из дисперсии.
Основные распределения случайной величины.
Равномерное распределение. Плотность вероятности такого распределения на некотором интервале постоянна.
Нормальное распределение зависит от математического ожидания и дисперсии. Плотность вероятного распределения выражается в виде экспоненциальной кривой. Нормальное распределение обладает важными свойствами: сохраняется при линейных преобразованиях случайных величин, является предельным для ряда других распределений или они к нему сводятся.
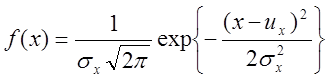
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.