Навигационные параметры и изолинии. Аналитический метод определения места судна с помощью изолиний. Линеаризация навигационных функций и ее геометрическая интерпретация. Априорная и апостериорная оценка точности обсервации, страница 4

Градиенты навигационных функций являются размерными величинами в зависимости от размерности самой функции. Если функция навигационного параметра представлена в сферических полярных координатах r и y, то главными компонентами градиента в этих координатах будут составляющие вдоль радиуса r и по нормали к нему. На рисун­ке показаны такие составляющие на сфере с полюсом сфери­ческих координат в точке PN.  Модуль составляющей g_j, изме­няется в зависимости от сферического радиуса или, что то же самое, от центрального угла r. Здесь действует непосредствен­ная аналогия с длиной дуги параллели, только угол «паралле­ли» отсчитывается не от экватора или любого другого большо­го круга, а от полюса.

Модуль градиента не зависит от выбора системы координат и определяется выражением:

                                                                                    (23)

Решение задачи определения координат обсервованного места судна обобщенным методом линий поло­жения предусматривает предварительное вычисление составля­ющих градиента. В этом случае коэффициенты уравнений типа 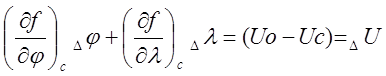 (24) станут известны, и задача определения места судна путем решения систем таких уравнений формально будет решена.

При предварительном расчёте градиента преследуются две цели:

во-первых, открывается поле широкого теоретического ис­следования различных навигационных функций, во-вторых, для практического решения заранее готовится массив коэффициен­тов уравнений ЛП.

В случае конкретных измерений тех или иных навигационных параметров делается выборка соответствующих значений градиентов для решения общей задачи определения места судна.

Модуль градиента:

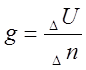                                                                                                (25)

Отсюда следует, что модуль градиента - есть характеристи­ка связи линейного смещения линии положения на поверхности и изменения навигационного параметра.

Исходя изданного определения сравнительно несложно по­лучить формулы модуля градиента и определить его размер­ность для различных навигационных изолиний. Так как гради­ент всегда направлен в сторону увеличения параметра по нор­мали к изолинии (т. е. перпендикулярно ЛП), то нетрудно ус­тановить и его ориентацию. Следовательно, будут определены все элементы линии положения.

Если в уравнении (24) обе части поделить на модуль градиента (U_o - U_c)/g = _DU/g и сопоставить это с формулой 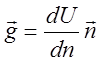, то можно получить строгое определение модуля градиента:

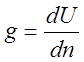                                                                                                 (26)

То есть бесконечно малому приращению навигационного параметра dU соответствует бесконечно малое приращение dn смещения линии положения по нормали к изолинии. Смещение Dn называют переносом линии положения из счислимого места в обсервованное,

Dn = DU/g = (U_o – U_c)/g.                                                          (27)

Соответственно и уравнение ЛП теперь можно записать, ис­пользуя понятие переноса, следующим образом:

costDj + sintDw =Dn.                                                            (28)                     

Такая форма широко распространена при графоаналитичес­ких способах решения задачи определения места судна, напри­мер в мореходной астрономии. Величины Dn и t называются элементами линий положения.

1.3.2  Градиенты навигационных функций

Рассмотрим некоторые частные градиенты.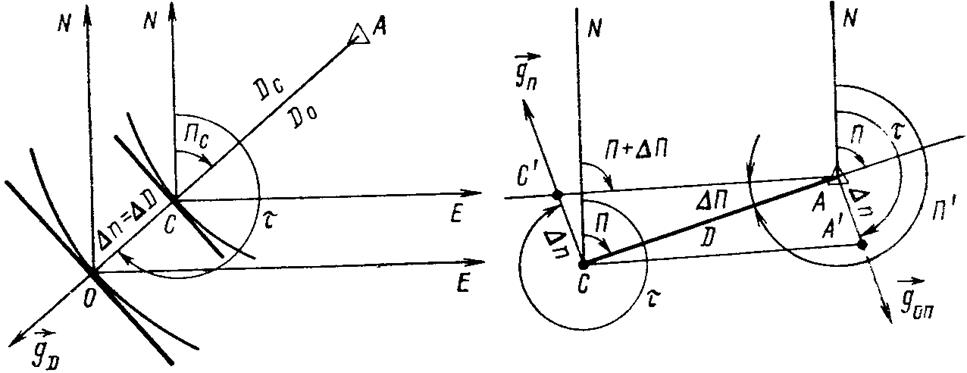      

Рис. 12. Градиент расстояния на плоскости                          Рис. 6.1'8. .Градиенты прямого и об ратного пеленгов

Градиент расстояния на плоскости (рис. 12). Пусть изме­рено расстояние Do и из счислимой точки С с карты снято счислимое значение Dc. Приращение навигационного параметра _DU = _DD, а смещение ЛП _Dn = _DD, следовательно, по формуле  g_D = l. Модуль градиента расстояния безразмерен, так как приращение параметра выражается в тех же единицах (милях, кабельтовых), что и смещение ЛП. Направлен гради­ент расстояния всегда вдоль счислимого пеленга в сторону уве­личения дистанции: t = П±180°. Знак «+» принимается при П<180°, знак «—» при П>180°.

Градиенты прямого и обратного пеленгов на плоскости(рис. 13). Измерен пеленг П с судна на ориентир в преде­лах малых расстояний. Такой пеленг называется прямым или просто пеленгом, а пеленг с маяка на судно П’=П+180⁰ - обратным пеленгом.

Сначала рассмотрим прямую задачу. Приращение пеленга означает его поворот на малый угол _DП. В результате такого разворота происходит кажущееся смещение счислимой точки С в положение C’ на значение переноса _Dn. Из прямоугольного треугольника АСС' получим значение этого переноса: _Dn =D*tg_DП. Вследствие малости приращения пеленга _DП можно приближенно принять вместо тангенса его собственный угол в радианах: tg_DП»_DП, тогда _Dn=D_DП.

Отсюда градиент

g_п=_DП/(_DПD)=1/D рад/миля.                                                                  (29)

Так как на практике пеленг выражается в градусах, эту формулу применяют в другой размерности (...^о/миля):

g_n =  57,37^о/D.

Значит, чем дальше судно от ориентира, тем больше его линейное смещение перпендикулярно пеленгу при одном и том же приращении пеленга: _Dn = D_DП.

Направление градиента пеленга в круговом счете всегда определяется равенством

t = П - 90°.                                                                                             (30)

Рассмотрим обратный пеленг. Для этого на рис. 13 доста­точно перенести отсчет пеленгов в точку Л. Приращение пеленга _DП и смещение счислимого места _Dn остаются прежними. Однако видно, что увеличение отсчета пеленга происходит в обратную сторону. Следовательно, направление градиента теперь следует также изменить на противоположное:

t = П+90°,                                                                                               (31)

Градиент горизонтального угла (рис. 14). Горизонтальный  угол a, изолиния которого является окружностью, на которую опирается этот угол, можно рассматривать как разность пеленгов двух ориентиров А и В. Это дает основание рассчитывать градиент горизонтального угла как разность векторов градиентов пеленгов каждого ориентира: