![]() (32)
(32)
Модули градиентов соответствующих пеленгов выразятся равенствами g1=gПА = 1/DА; g2=gПВ = 1/DВ.
Найденные абсолютные значения градиентов определяют длины двух сторон векторного треугольника. Вычислим третью сторону по формуле косинуса угла плоского треугольника:
![]() (33)
(33)
Раскрыв значения модулей градиентов и приведя к общему знаменателю, получим
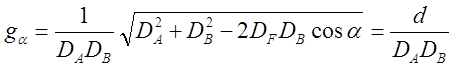 (34)
(34)
Выражение с радикалом представляет собой формулу косинуса стороны АВ плоского треугольника АВС, которая называется базисом d. Размерность модуля - радиан на милю. Горизонтальные углы иногда измеряются в минутах дуги секстаном, поэтому
ga = 57,3°d/(DA DB) ...°/мнля и ga =3438'*d/(DA DB) ...’/миля. (35)
Градиент горизонтального угла всегда направлен к центру окружности - изолинии угла a, т. е. по нормали к ней в сторону увеличения этого угла. Определять направление проще всего по графическому построению векторного треугольника градиентов в выбранном масштабе обратных расстояний.
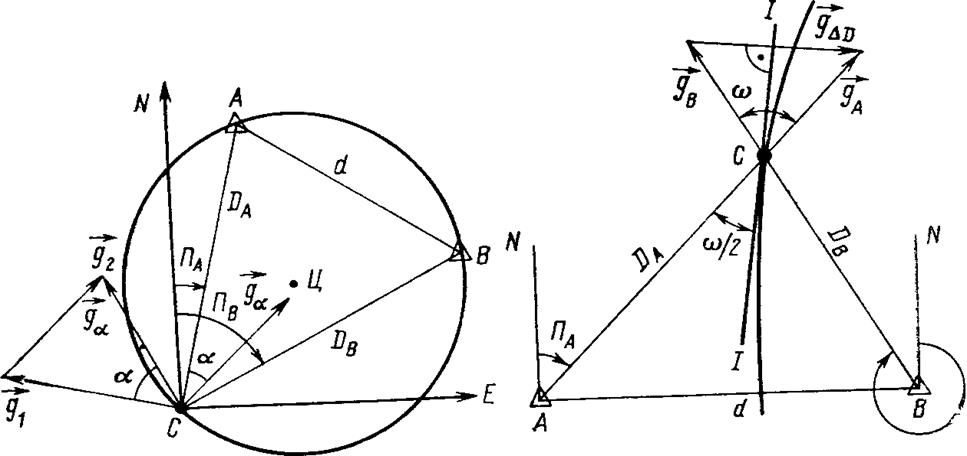
Рис. 14. Градиент горизонтального угла Рис. 15. Градиент разности растояний
Градиент разности расстояний (рис. 15). При выводе формулы данного градиента можно воспользоваться тем же приемом, который был применен при выводе градиента горизонтального угла. Полагаем, что градиент разности расстояний равен разности градиентов расстояний до каждого навигационного ориентира А , В. Тогда модуль градиента определится формулой (33), в которой следует понимать под обозначениями g1, g2 модули градиентов расстояний. Значение такого модуля равно единице, поэтому
![]() , (36)
, (36)
где w - угол между направлениями на ориентиры в счислимой точке С, часто называемый базовым.
Применяя формулу разложения квадратов тригонометрических функций по кратным дугам, получим
gDD = 2*sin(w/2) (37)
Направление градиента определим по рис. 6.20, где построен векторный треугольник градиентов. Так как треугольник равнобедренный (g1=g2=l), линия положения I - I, направленная перпендикулярно градиенту, одновременно является биссектрисой угла w, равного разности пеленгов Па, ПB на ориентиры. Направление градиента
t = (ПА+ПВ)/2±90о (38)
Знак «+» или «-» выбирают так, чтобы градиент был направлен в сторону увеличения разности расстояний DD = DA - DB, т. е. всегда в сторону ближайшего фокуса гиперболы.
Формулы (37) и (38) справедливы для плоскости и для сферической гиперболы. Этот вывод вытекает из равенства единице модулю градиента сферического расстояния и того факта, что касательная к сферической гиперболе делит базовый угол w пополам так же, как и в плоской гиперболе.
Градиент вертикального угла
Мы уже знаем, что изолиния вертикального угла - окружность на плоскости. Этот навигационный параметр используется для определения места судна по расстояниям до ориентиров с известной высотой, которые рассчитываются по вертикальному углу, измеренному секстаном.
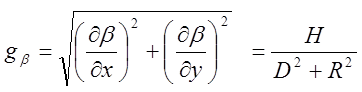 (39)
(39)
t = П (40)
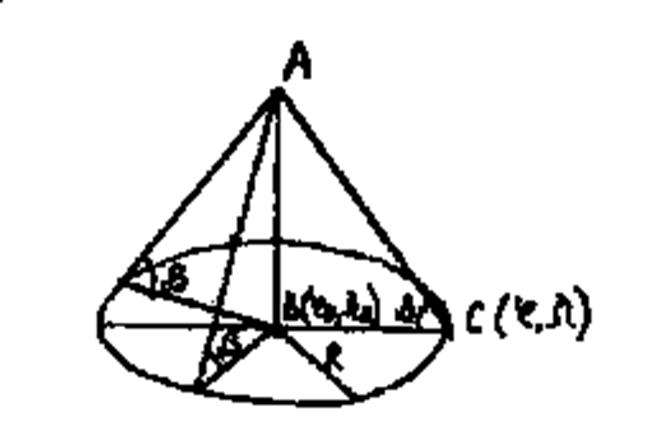
Рис. 16. Градиент вертикального угла
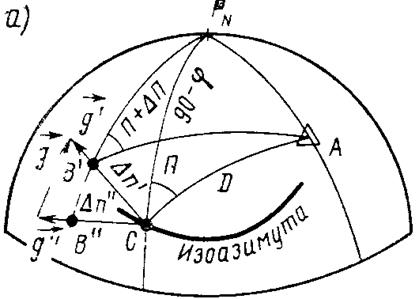
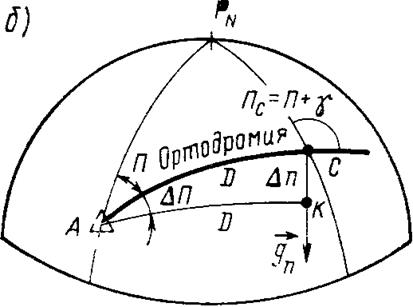
Рис. 17. Градиенты прямого (а) и обратного (б) пеленгов на сфере
Градиент прямого и обратного пеленгов на сфере. Градиенты пеленгов можно определить по приближенной формуле (25), если воспользоваться свойствами элементарных прямоугольных сферических треугольников.
Для вывода градиента прямого пеленга (рис. 17, а) будем рассматривать пеленг как разность направлений СА и СPN от точки С на ориентир и Северный полюс. Тогда, как и в случае горизонтального угла, можно считать градиент пеленга разностью градиентов направлений СА и СPN.
Применяя формулу косинуса стороны для плоского треугольника, образованного длинами градиентов, получим окончательную формулу модуля градиента прямого пеленга на сфере
![]() (41)
(41)
Зная теперь длины всех сторон треугольника градиентов и его ориентацию относительно меридиана, по формулам плоской тригонометрии можно вывести выражение для направления градиента пеленга
tgt =tgj/(ctgDsinП) – ctgП (42)
Если пеленг измерен в не слишком высоких широтах j и на малых расстояниях D, то допустимы следующие упрощения:
tg j << ctgD и ctg D » 1/D. В таком случае выражения (41) и (42) вырождаются в формулы градиента пеленга с судна на ориентир на плоскости (29) и (30).
Элементы градиента обратного пеленга (рис. 17,6) несложно получить из решения элементарного сферического треугольника АСК. В элементарном треугольнике малая сторона, противолежащая малому углу, может быть определена по формуле Dn = sin DDП. Отсюда, используя формулу градиента (6.48), получим
gП = DП/(sinDDП) = 1/sinD = cosecD (43)
Направление градиента в точке С с учетом сферического схождения меридианов
t = Пс+90° = П+g+90°. (44)
Еще этот метод называют Обобщенным методом линий положения или Итерационным методом последовательного приближению Ньютона.
Для осуществления этого метода необходимо измерить как минимум два навигационных параметра – Uo1 и Uo2, которые соответствуют двум линиям положения.
При определении понятия градиента были установлены все ocнoвныe и дoпoлнитeльныe условия замены изолинии на линию положения. Следовательно, можно перейти к задаче определения места на более реальной, чем метод изолиний основ. 'Решение данной задачи и носит назваяие обобщенного метода линий положения.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.