y0=(tg(30°)*tg(82°)*(3-8)+(tg(82°) *5-(tg(30°)*9)/(tg(82°)-tg(30°)=1.50 мили.
Подобные решения существует и при определении места судна другими способами: по двум расстояниям, двум горизонтальным углам, двум высотам светил (задача Гаусса), и т.д.
Основным недостатком прямого аналитического метода является отсутствие однообразия в исходных и расчетных формулах.
Формальный подход к решению систем со сложными уравнениями заключается в максимально возможном понижении порядка каждого уравнениями различных заменах переменных, способствующих такому понижению. В принципе любую, сколь угодно сложную, непрерывную функцию можно представить в виде линейного отрезка: вопрос лишь в том, от какой точки отложить данную линию и какова его длина, обеспечивающая отклонение по нормали от исходной функции не больше заданного значения x. Такое приближение функции называется линеаризацией.
Линеаризация навигационной изолинии облегчается одним весьма полезным обстоятельством, присущим практике мореплавания наверно уже в течение столетий: наличием счислимого места как естественной точки линейной аппроксимации. Аналитические методы приближения функций опираются на разложение заданных функций в различные ряды или аппроксимацию полиномами по формальным критериям.
В данном случае удобнее всего представить изолинию рядом Тейлора в окрестностях счислимой точки. Такая аппроксимация имеет ясный геометрический смысл - одномерная функция представляется в виде совокупности следующих элементов: постоянная величина (нулевое приближение), наклонная линия (первое приближение), парабола (второе приближение), кубическая парабола (третье приближение) и далее по возрастающим показателям степени с коэффициентами в виде произвольных возрастающего порядка.
Представим общее уравнение, изолинии в следующем виде:
F (j,l) - Uo = 0 (11)
Для получения линейного приближения достаточно ограничиться разложением функции двух переменных уравнения до первых членов ряда:
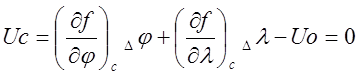 (12)
(12)
Здесь индекс «С» указывает на разложение в счислимой точке, т. е. частные производные вычисляются для координат счислимого места.
Величина Uc носит название счислимого навигационного параметра и рассчитывается по известным координатам счислимого места. Значения приращений аргументов разложения Dj и Dl определяют элементарное смещение географических координат от счислимой точки С до обсервованной точки О:
Dj = jо - jс (12)
Dl = lо - lс
И предыдущее уравнение записывают обычно так:
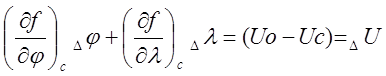 (13)
(13)
Здесь величина DU характеризует приращение навигационного параметра от счислимого значения к наблюденному (обсервованному).
Последнее уравнение описывает одно из важнейших понятий навигации - линию положения [ЛП], которая является касательной, к изолинии, проведенной в счислимом месте.
Полученное уравнение удобнее представлять в местной прямоугольной системе координат с началом в счислимом месте С и элементарными приращениями разности широт Dj и отшествия Dw. В этом случае
U = f(j,w) и уравнение ЛП принимает вид:
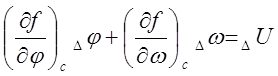 (14)
(14)
Особый смысл в уравнениях ЛП приобретают коэффициенты - частные производные изолинии по каждой из прямоугольных координат. Известно, что первые производные функции характеризуют скорость ее изменения. В данном случае по координатам j и w. Поскольку навигационный параметр образует скалярное поле, то скорость изменения его значений характеризуется векторной величиной - градиентом.
Таким образом, вектор-градиент навигационного параметра (DU = g) показывает скорость изменения навигационного параметра в конкретной точке поля. Градиент навигационного параметра всегда направлен по нормали к функции в заданной точке в сторону увеличения навигационного параметра
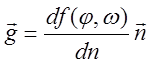 или
или
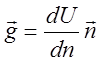 (15)
(15)
где n—единичный вектор нормали к изолинии, составленный ортами i— по оси j; j—по оси w
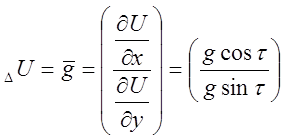 (16)
(16)
Отсюда нетрудно получить полярные компоненты вектора, т. е. его модуль g (длину) и направление t, относительно меридиана:
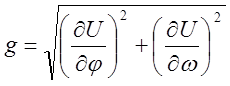 (17)
(17)
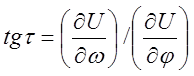 (18)
(18)
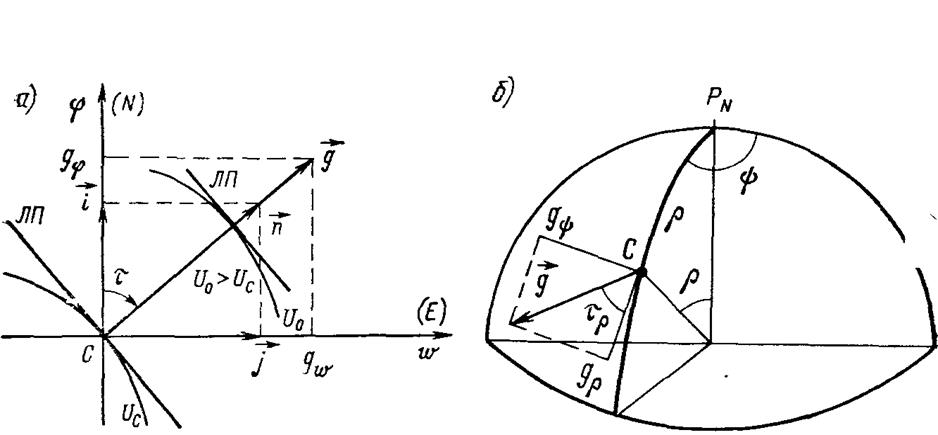
Рис.10 Градиент навигационного параметра в прямоугольных (а) и полярных сферических (б) координатах.
В декартовых координатах модуль градиента может быть представлен как
![]() ,
где (19)
,
где (19)
gj = dU/dj=g*cost; gw = dU/dw=g*sint; (20)
В географических координатах модуль g и направление t будут соответственно
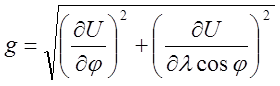 (21)
(21)
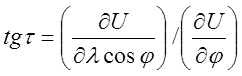 (22)
(22)
После введения понятия градиента становится ясно, что коэффициенты уравнений линии положения есть проекции градиента на оси координат, в которых представлено данное уравнение. В таком случае уравнение линии положения можно записать, как уравнение прямой в следующем обобщенном виде:
g costDj + g sintDw = DU
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.