Существующие, приборы, системы и традиционные методы определения места судна имеют значительные недостатки. Так, например, погрешности определения счислимых координат зависят от точности работы лага и компаса, от гидрометеорологических условий 'плавания, 'погрешности определения счислимых координат растут с течением времени. Методы мореходной астрономии зависят от погодных условий, имеют ограниченную точность, а также требуют значительного времени для получения обсервованных координат. Визуальные методы определения места судна имеют ограниченный район применения, и их использование также зависит от погодных условий. Радиопеленгование имеет ограниченный район использования и низкую точность. Почти все радионавигационные системы имеют ограниченный район использования, а глобальные радионавигационные системы имеют и низкую точность. Спутниковые навигационные системы на низких орбитах обладают значительной дискретностью определения места. Радиолокационные станции имеют ограниченный район использования и необходимость опознания ориентиров.
Список можно продолжить, но уже совершенно очевидно, что недостатки традиционных методов и средств определения места судна в значительной мере снижают безопасность мореплавания.
В соответствии с хорошей практикой любой инженерный расчет должен сопровождаться оценкой точности полученного результата: отыскание математического ожидания искомых параметров и их дисперсии. В судовождении при определении места судна рассчитывают координаты и оценивают их точность либо через ковариационную матрицу, либо через одну из ее геометрических интерпретаций, например в виде эллипса погрешностей.
Измерения проводятся с погрешностями, поэтому и обсервованные координаты вычисляются тоже с погрешностями.
Особенностью определения координат является тот факт, что измерения косвенные, то есть измеряются навигационные параметры, и допущенные погрешности затем переносятся в погрешности координат.
Для оценки точности обсервации используются вероятно-статистические методы, которые устанавливают границы некоторой доверительной области, в которой с заданной вероятностью может находиться истинное место судна. При этом делаются следующие допущения:
Рассмотрим этот вопрос на примере ОМС по двум измерениям. В этом случае линеаризованная система принимает вид.
A DX = DU(75)
Так как измерения с погрешностями, то перепишем систему в виде
A (DX+dx) = DU+du.(76)
Тогда
A dx = du.
Откуда
dx = A-1 du. (77)
Погрешности измерений могут быть статистически зависимы. Такая зависимость существует хотя бы потому, что обычно используются как минимум одни и те же инструменты. Эта статистическая зависимость определяется коэффициентом корреляции, а общее описание такой зависимости дает ковариационная матрица погрешностей измерений.
Формирование ковариационной матрицы погрешности измерений выполняется по формуле
D(Du)=du duT . (78)
Для двумерного случая это выглядит так:
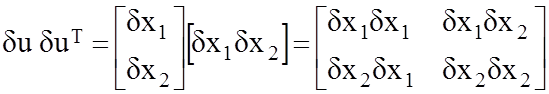
На главной диагонали находятся дисперсии измеряемых навигационных параметров, а вне диагонали - ковариационные моменты, которые характеризуют статистическую связь между измерениями.
Структура ковариационной матрицы погрешностей измерений определяет название МНК: если матрица диагональна и все ее компоненты равны, то алгоритм носит название МНК, если компоненты не равны, то это метод взвешенных наименьших квадратов; если матрица не диагональна, то это обобщенный МНК.
Погрешности измерений в процедуре расчета трансформируются в погрешности координат. В качестве такого преобразователя погрешностей используется матрица коэффициентов A.
Определим ковариационную матрицу погрешностей определяемых параметров, используя правила (A B)-1 = B-1 A-1 и (B-1)T=(BT)-1
D(Dx)=dx dxT = (A-1 du) (A-1 du)T =A-1 du duT (A-1)T =
A-1 D(Du) (A-1)T = (AТ (D(Du))-1 A)-1.
В дальнейшем при написании ковариационных матриц, где это не вносит двузначности, будем опускать аргумент
Обозначим ковариационную матрицу погрешностей координат через
N= D(Dx) = (AТ D-1 A)-1. (79)
Для двумерного случая матрица N имеет вид:
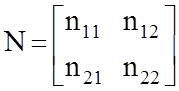 ,
,
где n11 - дисперсия по широте
n22 - дисперсия по отшествию.
n12 = n21 - ковариационные моменты.
Вся информация о погрешностях содержится в матрице N . В судовождении часто используется ее геометрическая интерпретация в виде эллипса погрешностей. Установим связь между элементами матрицы N и параметрами эллипса: полуосями и углом ориентации.
В общем случае такая задача рассматривалась Хоттелингом Г. в 1933 г. Было показано, что для ковариационной матрицы существуют векторы, направлениям которых соответствуют максимальные и минимальные значения рассеивания (погрешностей). Численно эти значения соответствуют собственным числам матрицы. Направления собственных векторов, указывающие на направление максимального и минимального рассеивания (дисперсии), соответствуют направлениям полуосей эллипса. Собственные числа - это экстремальные значения дисперсий. Для перехода к линейным величинам - полуосям эллипса (гипер - эллипса для n-мерного пространства), необходимо извлечь квадратный корень.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.