Навигационные параметры и изолинии. Аналитический метод определения места судна с помощью изолиний. Линеаризация навигационных функций и ее геометрическая интерпретация. Априорная и апостериорная оценка точности обсервации, страница 2

Изолиния разности расстояний на сфере. Обозначим симво­лом а расстояние на поверхности Земли между ориентирами А и В. Это расстояние называется базой.

        

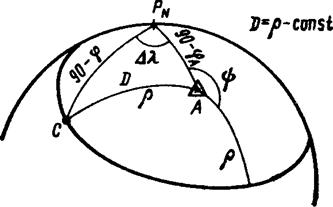
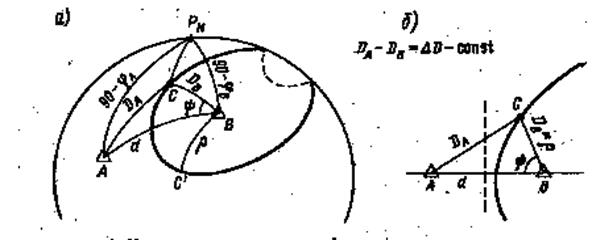
Рис.5 Сферическая изостадия                                  Рис.6 Изолиния разности расстояний

Уравнение плоской гиперболы в полярных координа­тах:

r = (d² - DD²)/(2*(DD + d*cosy))                                           (10)

Отличие сферической гиперболы от плоской - в силу всегда соблюдаемого неравенства DD<d существуют условия, при которых радиус r плоской гиперболы неограниченно возрастает, и ее ветви уходят в бесконечность. Однако для сферической гиперболы таких условий нет, поэтому r®90°.

Следовательно, изолиния разности расстояний на сфере в  отличие от изолинии на плоскости есть всегда замкнутая ограниченная кривая.

1.2  Аналитический метод определения места судна с помощью изолиний.

1.2.1  Теория

Для определения места судна необходимо измерить, как минимум два навигационных параметра U₁ и U₂ изолинии которых имеют общую точку пересечения O с координатами j_o и l_о

U₁ = f₁(j_o, l_о)

U₂ = f₂(j_o, l_о)

Такая точка называется обсервованным местом судна,  а широта j_o  и долгота l_о - обсервованными координатами.

Возможны два пути решения данной задачи: графический и аналитический.

Графическое решение заключается в построениина карте участков навигационных изолиний в предполагаемом месте судна. Обычно такой точкой является счислимое место судна С, определенное по лагу и компасу после внесения всех предполагаемых поправок. Данный способ удобен для штур­манской практики и дает быстрое и наглядное решение прямо на путевой карте. Проложив два пеленга или два расстояния  или пеленг и расстояние посредст­вом штурманского прокладочного инструмента, находят точку пересечения изолиний и при необходимости снимают координа­ты этой точки с рамок карт.

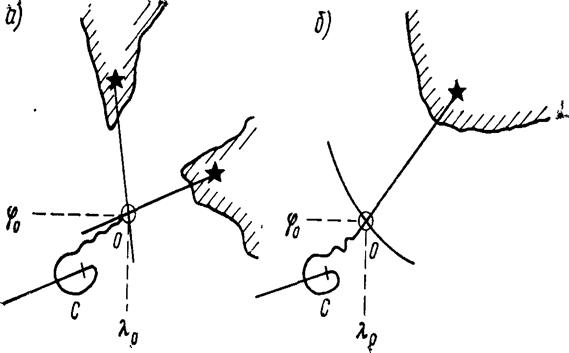
Рис.8. Графическое определение места судна                                    Рис.9 Сетка навигационных изолиний.

При плавании в узкостях или других стесненных районах плавания иногда предварительно строят сетку навигационных изолиний, по которой можно оценивать место без прокладки, если на сетке нанесена оцифровка значений навига­ционных параметров. Довольно распространен способ направ­ляющей изолинии, когда удается совместить изолинию навига­ционного параметра с направлением пути судна.

При всех достоинствах графического способа определения места он доступен лишь для простых по форме изолиний и по своей сути индивидуален для каждого типа навигационного па­раметра. Во время плавания судоводители не в состоянии стро­ить такие сложные навигационные изолинии, как ортодромии изостадии, изопеленги и гиперболы на кар­тах меркаторской проекции. Для разностно-дальномерных РНС выпускают специ­альные карты с нанесенной сеткой изолиний, где место судна находят путем линей­ной интерполяции между значениями навигационного параметра. Однако в це­лом, учитывая и время из­мерения параметра, графи­ческая процедура обсерва­ции продолжительна и, глав­ное, плохо поддается фор­мализации для того, чтобы ее можно было автоматизи­ровать.

Аналитический путьрешения задачи определения места судна исходя из уравнений общего вида

U₁ = f₁(j_o, l_о)                   (9)

U₂ = f₂(j_o, l_о)

на первый взгляд выгодно отличается от графического решения своей уни­версальностью. С формальной точки зрения, необходимо наити корни системы двух уравнений, т. е. решить обращенную систему вида

j_о = F₁(U_o1, U_o2)              (10)

l_o = F₂(U_o1, U_o2)

Единственное строгое требование здесь заключается в непре­рывности функций U₁ и U₂ заданных фиксированными значе­ниями U_o1 ,U_о2. Однако в реализациях такого подхода и появляются главные трудности прямого аналитического метода.

Решение данных систем, в которых невозможно получить однозначные решения уже в силу периодического характера функций искомых величин, довольно сложная задача. Кроме того, после приведения этих уравнений об­наруживается их трансцендентный характер, при котором иско­мые координаты присутствуют в неявном виде, скрываясь под круговыми функциями со сложными аргументами.

Таким образом, недостатками прямого аналитического метода являются:

а) невозможность получения однозначного решения в силу периодичности функций искомых величин;

б) трудность получения результатов в явном виде относительно обсервованных координат.

 Все это вместе не позволяет добиться решения без какого-либо началь­ного приближения даже при использовании современных высо­коэффективных численных методов. Таким образом, становится совершенно очевидным  единственный вариант реализации ана­литического метода в судовых средствах вычислительной тех­ники: провести линеаризацию исходных уравнений в окрестнос­тях какой-либо точки, которая может играть роль достаточно обоснованного начального приближения места судна. Только тогда аналитическое решение задачи определения места судна, обладая высокой универсальностью, необходимой, прежде всего в навигационных автоматизированных комплексах, приобретает реальное, надежное и эффективное математическое обоснова­ние.

1.2.2  Алгоритм решения задачи расчета координат по 2 измерениям (прямое аналитическое решение)

Прямое аналитическое решение таких задач сводится к (10) и имеет достаточно сложный вид даже для простых навигационных функций. Рассмотрим задачу определение места по двум пеленгам на плоскости.

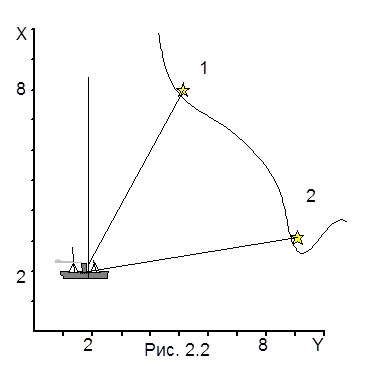
              Система 9, в соответствии с Рис 2.2 будет иметь вид:

tgП₁=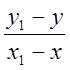tgП₂=

где х₁ ,х₂, y₁, y₂ – координаты ориентиров. Обозначив tg(П₁) через Т₁,а tg(П₂) через Т₁, получим:

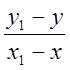
Т₁(х₁–х₀)-y₁ = Т₂(х₁–х₀)–y₂;

х₀=(Т₂х₂-Т₁х₁+y₁–y₂)/(Т₂-Т₁);

y₀=(Т₁Т₂(х₂-х₁)+Т₂y₁–Т₁y₁)/(Т₂-Т₁);

пусть П₁=30°, П₂=82°, тогда

х₀=(tg(82°)*3-tg(30°)*8+5-9)/(tg(82°)-tg(30°))=1.95 мили