Навигационные параметры и изолинии. Аналитический метод определения места судна с помощью изолиний. Линеаризация навигационных функций и ее геометрическая интерпретация. Априорная и апостериорная оценка точности обсервации, страница 6

Итак, есть два измеренных навигационных параметра U_o1 и U_o2 и счислимые координаты j и l, для которых можно рассчитать счислимые значения этих параметров:

g₁ cos t₁Dj + g₁ sint₁Dw - (U_o1 - U_c1) = 0                             (45)

g₂ cos t₂Dj + g₂ sint₂Dw - (U_o2 - U_c2) = 0

Введем для простоты записи следующие обозначения, кото­рые будут применяться и в дальнейшем:

a_i = g_i cos t_I; b_i = g_i sin t_I                                                                                                                      (46)

l_i = -DU_i = U_ci - U_oi

Используя данные обозначения, систему уравнений приведем к виду, стандартному для формализации определения места судна:

a₁ Dj + b₁ Dw + l₁ = 0                                                                            (47)

a₂ Dj + b₂ Dw + l₂ = 0

Существуют два способа решения задачи определения координат места судна по данным уравнениям: аналитический и графоаналитический.

Аналитическое решение заключается в следующем:

Принимая в качестве первого приближения счислимые координаты j_с , l_с будем искать решение в виде:

j_о =j_с+Dj_с.

l_о =l_с+Dl_с .                  (48)

Решение считается полученным, когда значенияj_о, l_оподставленные в выражения для навигационной функции дадут значения измеренных навигационных параметров.

Разложим правую часть системы (48) в ряд Тейлора в счислимой точке и ограничимся линейными членами (49):

Получена система линейных уравнений относительно поправокDj  и Dlк счислимым координатам

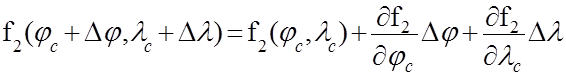
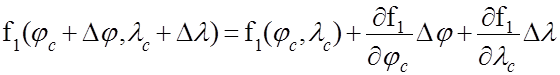U_О1–U_C1= 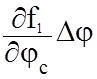 +  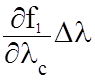                    (50)

U_О2–U_C2 =  +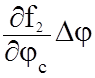

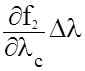
где         f _I(j_с + Dj_с, l_с + Dl_с) = U_Оi - измеренные значения навигационных параметров

f _I(j_с, l_с) = U_CI - счислимые значения навигационных параметров.

Решая систему (50) находим Dj  и Dl. Данная вычислительная процедура итерационная. Уточненные значения координат для текущей итерации определятся в соответствии с (48).

Если необходимая точность решения не достигнута, то выполняется следующая итерация, т. е.:

- Счислимым координатам присваиваются обсервованные значения.

j_с = j_о,  l_с = l_о.

-   Формируется и решается система (50).

Здесь подстрочные индексы «о» и  «с», как и ранее, соответствуют понятиям  “обсервованный” и «счислимый»

Для прямоугольной системы координат (50) запишется так:

U₀₁- U_c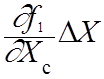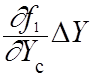1    =  +                    (51)

U₀₂- U_c2 = +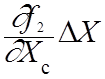

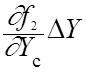
Или в следующем виде:

            a₁₁ Dx + a₁₂ Dy = DU₁                          (52)

            a₂₁ Dx + a₂₂ Dy = DU₂ ,

где a_ij - соответствующие частные производные.

Решение отыскивается в виде аналогичном (48)

x_о = x_с +Dx

y_о = y_с +Dy                               (53)

Смысл условных обозначений ясен из ранее написанных формул.

Геометрический смысл (2.6) очевиден. Это две пересекающиеся прямые. Если первое уравнения отнормировать множителем g₁=, а второе g₂=,то получим уравнения прямых в нормальной форме (54).

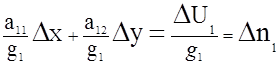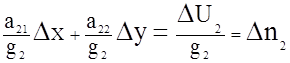Коэффициенты а_ij/g_i, станут направляющими косинусами. Одновременно изменится размерность правой части. Например, если взять навигационную функцию пеленга, то значения навигационного параметра будет в радианах. Размерность производной - рад/миля, а размерность нормирующего множителя миля/рад. Тогда правая часть - Dn_i ,будет в милях. Величина Dn_i равна кратчайшему расстоянию от начала координат до прямой. В нашем случае за начало координат принимается счислимая точка. В навигации такие уравнения принято называть линиями положения, а Dn_i - переносами линий положения. Рис. 2.2

1.4.2  Алгоритм решения задачи расчета координат места судна по 2 измерениям методом последовательных приближений (метод Ньютона)

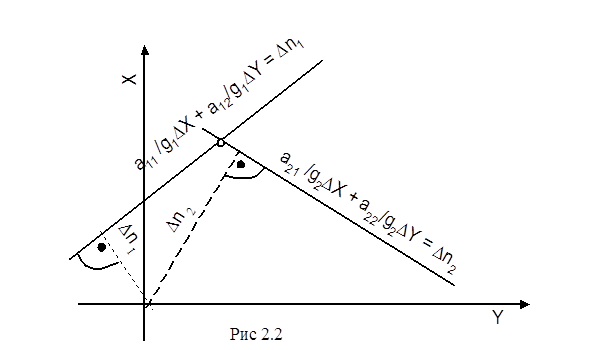
- измерить навигационные параметры Uo₁, и Uo₂„

- найти счислимыё значения Uc₁ и Uc₂ этих же навигационных параметров по счислимым координатам (j_с и l_с на момент измерений;

- вычислить приращения навигационных параметров DU₁ и DU₂, рассчитать модули градиентов g₁, g₂  и их направления τ_ι, t₂,

- вычислить коэффициенты системы уравнений

a₁ Dj + b₁ Dw + l₁ = 0                                                                            (55)

a₂ Dj + b₂ Dw + l₂ = 0 ;

- решить систему уравнений относительно неизвестных Dj и Dw:

Dj = (b₁l₂ – b₂l₁)/(a₁b₂ – a₂b₁)  ;                                              (56)

Dw = (l₁a₂ – l₂a₁)/(a₁b₂ – a₂b₁) (6.47)

вычислить географические координаты обсервованного места:

j_o = j_c +Dj                                                                                             (57)

l_j = l_c + Dw secj_т

Аналитическое решение обычно лежит в основе алгоритмов определения места по двум ЛП на штурманских калькуляторах и простейших персональных компьютерах.

Решения такого типа обычно применяют в мореходной астрономии и специальных задачах навигации.

Обобщенный метод линий положения некритичен к погрешностям задания счислимого места. Если счислимые координаты расположены близко от искомых обсервованных, то однократное аналитическое решение дает вполне приемлемый результат. В случае значительного удаления счислимой точки от обсервонной прибегают к итерационной процедуре определения места. Суть такого способа заключается в следующем: после первого цикла решения задачи выполняют проверку отклонения полученных координат от счислимых:

j_о - j_с = Dj£e₁                                                                                                                       (58)

l_о - l_с = Dl£e₂;

Здесь e определяется необходимой точностью решения задачи. Если приращения географических координат отвечают этим равенствам, то решение задачи заканчивается, если нет, то полученные координаты записывают как счислимые, и цикл счета повторяется. Процедуру выполняют до тех пор, пока равенства не будут удовлетворены. Обычно во всех алгоритмах определения места судна предусмотрена данная циклическая схема расчета. Как правило, итерационный процесс включает не более трех циклов.

1.4.3  Пример.