Навигационные параметры и изолинии. Аналитический метод определения места судна с помощью изолиний. Линеаризация навигационных функций и ее геометрическая интерпретация. Априорная и апостериорная оценка точности обсервации, страница 10

Для двумерного случая можно получить простые формулы. Запишем

n₁₁z₁ + n₁₂z₂ = lz₁

n₂₁z₁ + n₂₂z₂ = lz₂ (80)

или,

(n₁₁-l)z₁ + n₁₂z₂ =0

n₂₁z₁ + (n₂₂-l)z₂ =0  

или в матричном виде:

(N - lE) z = 0                                                                                           (81)

где.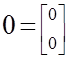

Чисто формально:

.

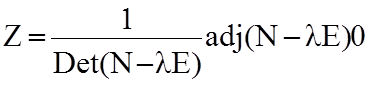следовательно,.

Так как Z произвольный вектор и, в общем случае не нулевой, то

Запишем для двумерного случая.

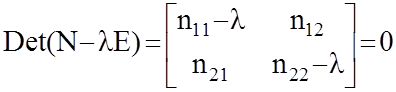
(n₁₁ - l) (n₂₂ - l) - n₂₁ n₁₂ = 0

Это квадратное уравнение. Решая его относительно l и, принимая во внимание, что n₂₁ = n₁₂ , так как матрица N симметрическая, получим:

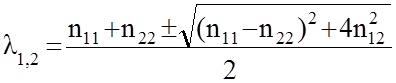                                  (82)

Определим ориентацию собственных векторов, соответствующих найденным собственным значениям. Считая l известным, подставим это значение в (80) и разрешим эту систему относительно z₁ и z₂,учитывая, чтоz₁= cos(Y), z₂= sin(Y)   .

Первое уравнение системы (80) будет выглядеть так:

n₁₁cos(Y) + n₁₂sin(Y) = l cos(Y)

Разделим первое левую и правую часть на cos(Y).

n₁₁ + n₁₂tg(Y) = l

Откуда

tg(Y) =(l - n₁₁)/ n₁₂(83).

Y = arctg ((l - n₁₁)/ n₁₂)(84).

Таким образом, фактически получено направление большой полуоси эллипса Y относительно норда. Если в 3.10 подставить другое значение l  то получим направление малой полуоси, но так как они ортогональны, то практически это не требуется.

Для отыскания полуосей необходимо извлечь квадратные корни из собственных чисел.

                               (85)

Когда говорят об оценке точности, то обычно добавляют слова априорная или апостериорная. Априорная - это оценка точности, выполненная по информации о погрешностях измерений полученной ранее. Как правило, такая информация о точности измеряемых навигационных параметров основывается на многочисленных статистических исследованиях, которые происходили до конкретной обсервации в каких-то осредненных условиях. Именно такая информация, как правило, содержится в ковариационной матрице погрешностей измерений используемой при расчете координат. В формуле (74) она обозначена как D . Если погрешности измерений статистически независимы, то внедиагональные элементы равны нулю и матрица имеет вид:

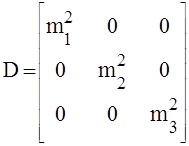
Именно эти погрешности в соответствии с правилом переноса погрешностей и формируют априорную ковариационную  матрицу определяемых параметров.

              Процедура построения эллипса погрешностей по ковариационной матрице сводится к следующему.

·  Рассчитываем собственные значенияlпо формуле (82)

·  Определяем угол ориентации Yпо формуле (84)

·  Рассчитываем полуоси по(85)

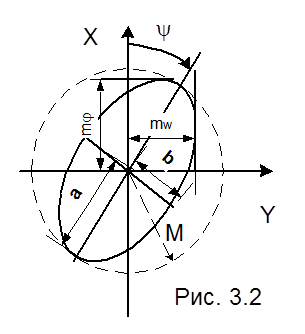
На рис. 3.2 показана связь между элементами ковариационной матрицы и эллипсом. Отрезок, заключенный между касательной к эллипсу параллельной оси Y и самой осью соответствует СКП по широте, или      (86)

Отрезок на оси Y , отсекаемый вертикальной касательной соответствует СКП по отшествию         (87)

              На рисунке также показана средняя квадратическая погрешность (СКП) обсервации М, которая  рассчитывается, как корень квадратный из следа ковариационной матрицы либо с помощью полуосей эллипса (88):

1.6.3  Апостериорная оценка точности

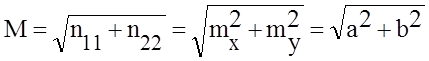
В априорной оценке использовалась информация о точности, полученная по результатам предыдущих измерений, а в апостериорной оценке участвуют текущие измерения, т.е. по которым была вычислена вероятнейшая точка.

              Допустим, что ковариационная матрица погрешностей измерений D известна с точностью до постоянного множителя:

D=m²K; D^-1=K^-1/m²;        K^-1= m²D^-1:

где матрица K известна, а величина m² неизвестна.

Иными словами известны относительные, а не абсолютные значения матрицы D. С учетом этого рассмотрим систему нормальных уравнений

                      (89)

Подставим вместо D^-1 выражение

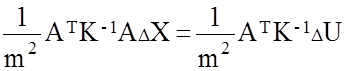
Величина m² (дисперсия наблюдения с единичным весом) сокращается и решение, в итоге, не зависит от абсолютной величины элементов ковариационной матрицы измерений D . Матрицу K^-1 также называют "весовой" и обозначают через W ,а m² - дисперсией наблюдения с единичным весом. Если m² не выносилась из D , то весовой будет просто D^-1.

Рассмотрим величину

  (90)

Она представляет собой обобщенную (взвешенную) остаточную сумму квадратов уклонений. Здесь M - операция взятия математического ожидания. Упрощенно ее можно рассматривать как отыскание среднего значения

              Рассмотрим выражение в последней скобке, то есть пока без операции взятия матожидания:

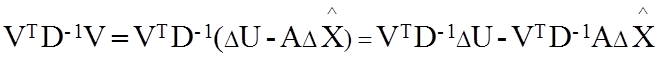          (91)

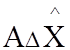Последнее слагаемое равно 0. Векторы  и    ортогональны, а скалярное произведение таких векторов равно 0. Тогда

                                                              (92)

Кроме этого,

              (93)

Во втором слагаемом произведение  представляет собой правую часть системы нормальных уравнений, тогда вместо нее запишем левую , тогда окончательно получим:

                            (94)

По этой формуле можно посчитать значение квадратичного критерия (остаточную сумму квадратов невязок). Здесь DU - вектор, рассчитанный по исходным данным U_И - U_c и первое слагаемое в правой части дает значение остаточной суммы в начальной (счислимой) точке, а второе слагаемое уменьшает это значение за счет смещения к оптимальной точке на величину .

С учетом взятия операции матожидания (94) справедливо следующее:

                              (95)

Распишем первое слагаемое:

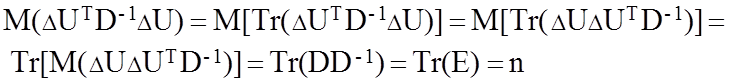              (96)

Правило  легко проверяется простым перемножением матриц небольшой размерности.

Распишем второе слагаемое:

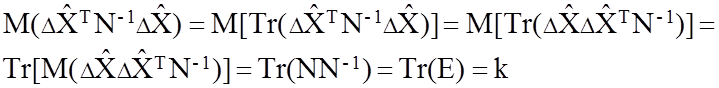                            (97)

С учетом (95) получим:

                                                                                                          (98)

Несмещенная оценка  дается выражением:

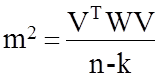                                                                                                                            (99)

Тогда апостериорную оценку ковариационной матрицы погрешности результатов получим следующим образом:

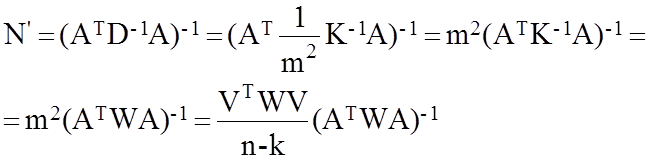                          (100)