Навигационные параметры и изолинии. Аналитический метод определения места судна с помощью изолиний. Линеаризация навигационных функций и ее геометрическая интерпретация. Априорная и апостериорная оценка точности обсервации, страница 12

Логарифмическое нормальное распределение получается в том случае, если логарифм случайной величины lnx имеет нормальное распределение.

Распределение Релея является распределением амплитуд суммы гармонических колебаний со случайными фазами. Применяется для описания характеристик колебательных процессов.

Распределение Лапласа, называемое также двусторонним экспоненциальным, имеет нулевое математическое ожидание и плотность вероятности с одним параметром. Кривая такого распределения имеет острую вершину и «приподнятые хвосты» - увеличенную вероятность больших погрешностей.

1.8.3  Учет систематических погрешностей при определении места судна

В отдельных случаях обсерваций необходимо оценить сме­щение места судна под действием предполагаемых системати­ческих ошибок измерителей. В частности, такая задача может ставиться при планировании рейса на этапе предварительной прокладки для оценки всевозможных, в том числе наихудших для безопасности мореплавания, смещений при прохождении узкостей.

Рассмотрим ситуацию возникновения систематического сдви­га обсервованной точки (рис. 6.27). В результате действия сис­тематических ошибок l₁, l₂ в измеренных навигационных пара­метрах место судна кажущимся образом переместилось из по­ложения О в точке О'. Смещение s можно считать равнодейст­вующим независимых смещений w₁ и w₂ линий положения одна по другой. В этом отношении w₁ и w₂,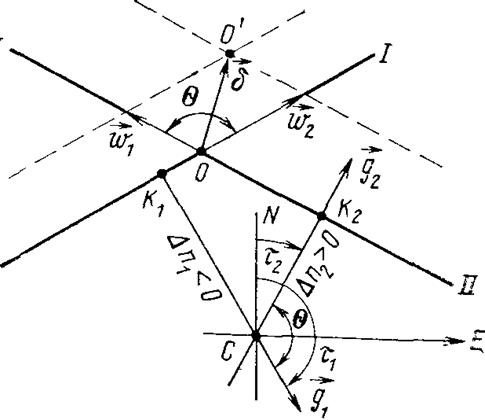

Рис. 21. Графоаналитический способ определения смещения места судна под действием систематических погрешностей измерителей

являются аналогами векториальных   ошибок, отличаясь лишь жестко  фиксированным на­правлением в соответствии с заданным знаком систематиче­ских погрешностей l₁, l₂. Опи­раясь на такую аналогию, можно получить следующие расчет­ные выражения для величин смещений ЛП:

D_ЛП2 = l₁/g₁;          D_ЛП1 = l₁₂/g₂                                                                                                        (103)

w₁ = D_ЛП1/sinq; w₂ = D_ЛП2/sinq;

Величину s определим как модуль вектора, построенного на векторах w₁ и w₂ с угломq между этими векторами. Запишем равенство s=w₁ +w₂ и составим скалярные произведения век­торов в левой и правой частях, т. е. вычислим проекции одного вектора по другому:

Отсюда длина результирующего вектора определится фор­мулой

             (104)

Из рис. 21 и формулы (104) видно, что важно брать угол q именно между направлениями w₁ и w₂. Если угол между век­торами острый (cosq>0), то вектор смещения о по модулю больше, чем при тупом угле (cosq<0). Отсюда следует, что в задаче оценки систематических смещений места судна всегда требуется рассчитывать q, как угол между направлениями гра­диентов ЛП, а не самих линий положения.

Подставив в формулу (104) вспомогательные формулы (103), получим результирующее выражение оценки величины смещения обсервованного места под влиянием систематических погрешностей измерений

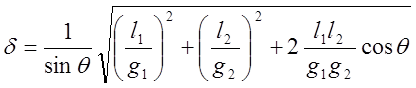(105)

Следующей, весьма важной задачей, связанной с система­тическими погрешностями места судна, является исключение влияния неизвестных систематических погрешностей измерите­лей на определение места судна. В решении данной задачи воз­можны два варианта, которые базируются на различных путях решения системы уравнений линий положения типа (45). Не­обходимым условием здесь выступает минимальная избыточ­ность измерений навигационных параметров, т. е. требование, по крайней мере, еще одной линии положения, в которой есть то же самое неизвестное, но постоянное смещение D_ЛП =const.

Система таких уравнений с учетом деления каждого из уравнений на модуль своего градиента может быть представле­на в следующем виде:

Dj cos t₁ + Dw sin t₁ + D_лп = Dn₁

Dj cos t₂ + Dw sin t₂ + D_лп = Dn₂                                                                         (106)

Dj cos t₃ + Dw sin t₃ + D_лп = Dn₃

Совершенно ясно, что три неизвестных однозначно опреде­лятся из трех уравнений, следовательно, будут найдены не только поправки счислимых координат, но и систематическое смещение линий положения. Через значение модулей градиен­тов могут быть найдены и достоянные погрешности навигацион­ных параметров.

Решить данную систему уравнений можно различным образом: методом последовательного исключения Гаусса, через определители по формулам Крамера или численными методами, связанными с процедурами последовательных приближений.

Второй вариант борьбы с систематическими погрешностями предусматривает формирование так называемой разностной, линии положения (РЛП). Вычитая в системе (6.82) из уравнении первой ЛП последовательно уравнения второй и третьей ЛП, получим систему из двух РЛП, где систематическая погреш­ность линий положения исключена:

(cos t₁ – cost₂)Dj + (sint₁ - sint₂)Dw = Dn₁ - Dn₂                             (107)

(cos t₁ – cost₃)Dj + (sint₁ - sint₃)Dw = Dn₁ - Dn₃

Принцип РЛП широко используется в навигации. Например, существует задача обсервации по трем пеленгам навигацион­ных ориентиров, когда не известна поправка компаса DК.  В этом случае можно перейти к определению места по двум го­ризонтальным углам, каждый из которых есть разность соот­ветствующих пеленгов:

a = КП₁ – КП₂ = (ИП₁ - DК) – (ИП₂ - DЛ) = ИП₁ – ИП₂          (108)

b = КП₁ – КП₃ = (ИП₁ - DК) – (ИП₃ - DЛ) = ИП₁ – ИП₃

Видно, что неизвестная поправка компаса здесь полностью исключается из преобразованного навигационного параметра. Подобный подход эффективен только в том случае, когда сис­тематическая погрешность существенно превалирует над слу­чайной.

Принцип разностных ЛП положен в основу разностно-дальномерных РНС, где компенсируется часть систематической по­грешности, вызванной неизвестным значением скорости распро­странения электромагнитных волн, несущих информацию о дальности до навигационных ориентиров. Переход к разности расстояний позволяет значительно снизить влияние неточного знания скорости света в реальных условиях. До конца устра­нить такую погрешность все же не удается ввиду расположения трасс распространения волн с различным сочетанием состояний поверхности «море—суша».