При формировании ![]() , начиная со старшего разряда
, начиная со старшего разряда ![]() , необходимо определить, на какой
"половине"
, необходимо определить, на какой
"половине" ![]() интервала
интервала ![]() изменения аргумента находится его
текущее значение
изменения аргумента находится его
текущее значение ![]() (см. рис. 1.12), и в соответствии
с этим сформировать значение
(см. рис. 1.12), и в соответствии
с этим сформировать значение ![]() , а также выделить
на ней диапазон изменения
, а также выделить
на ней диапазон изменения ![]() в виде разности
в виде разности ![]() , на основе которой будет найдено
значение более младшего бита (
, на основе которой будет найдено
значение более младшего бита (![]() ) кода
) кода ![]() .
.
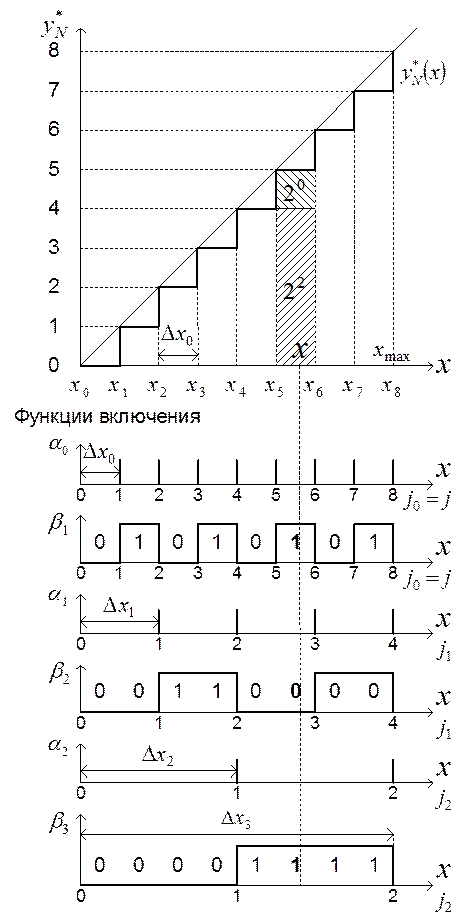
Рис. 1.12. Зависимости ![]() ,
,
![]() и
и ![]() для
формирования 3-битного кода
для
формирования 3-битного кода ![]() , когда
, когда ![]()
Реализация этих действий осуществляется путем выполнения операций:
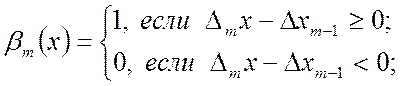
![]() ,
,
где ![]() ;
; ![]() – двоично-взвешенное эталонное
значение (вес), с которым для получения
– двоично-взвешенное эталонное
значение (вес), с которым для получения ![]() сравнивается
преобразуемая аналоговая величина
сравнивается
преобразуемая аналоговая величина ![]() .
.
В общем случае при
взвешивании, начиная со старшего разряда ![]() ,
функция включения
,
функция включения ![]() и разность
и разность ![]() последовательно определяются путем
вычисления:
последовательно определяются путем
вычисления:
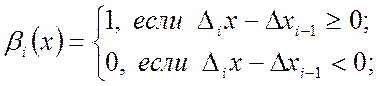 (1.19)
(1.19)
![]() , (1.20)
, (1.20)
где ![]() ;
;
![]() ;
; ![]() –
номера разрядов
–
номера разрядов ![]() эквивалента
эквивалента ![]() .
.
Нейроподобная структура
преобразователя ![]() (рис. 1.13), реализующего
последовательно совокупность зависимостей (1.19) и (1.20), содержит
(рис. 1.13), реализующего
последовательно совокупность зависимостей (1.19) и (1.20), содержит ![]() преобразующих нейроузлов, число
которых связанно с погрешностью преобразования
преобразующих нейроузлов, число
которых связанно с погрешностью преобразования ![]() в
соответствии с выражением (1.14). Узел
в
соответствии с выражением (1.14). Узел ![]() нулевого
каскада формирует набор весов
нулевого
каскада формирует набор весов ![]() , необходимых для
взвешивания преобразуемой величины
, необходимых для
взвешивания преобразуемой величины ![]() . Нейроузлы
. Нейроузлы ![]() –
– ![]() преобразующих
каскадов находят значения бит
преобразующих
каскадов находят значения бит ![]() для цифрового
эквивалента
для цифрового
эквивалента ![]() (1.18). Причем
(1.18). Причем ![]() для старшего
для старшего ![]() ‑го разряда
‑го разряда ![]() формируется на
выходе первого нейроузла
формируется на
выходе первого нейроузла ![]() , а
, а ![]() –
последнего
–
последнего ![]() .
.
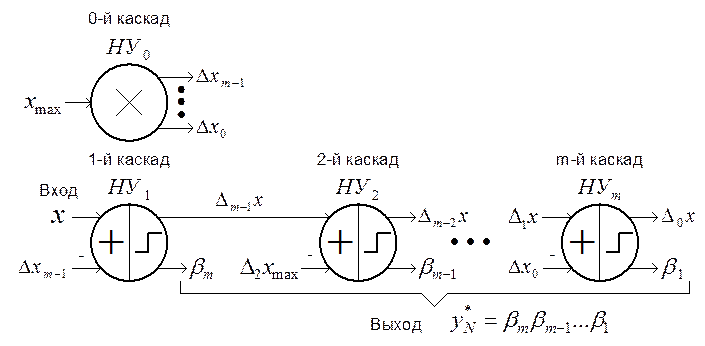
Рис. 1.13.
Нейроподобная структура Пр ![]() на основе метода
взвешивания, начиная со старшего разряда (1.19) и (1.20)
на основе метода
взвешивания, начиная со старшего разряда (1.19) и (1.20)
Время преобразования ![]() для нейроподобной структуры ПФИ
для нейроподобной структуры ПФИ ![]() со взвешенным кодированием (рис.
1.13) определяется как сумма затрат времени
со взвешенным кодированием (рис.
1.13) определяется как сумма затрат времени ![]() на
получение
на
получение ![]() функций включения
функций включения ![]() :
:
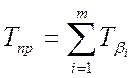 . (1.21)
. (1.21)
Принцип формирования
функций включения ![]() , начиная со старшего
разряда, наиболее широко используется при построении преобразователей частоты и
напряжения в позиционный код. При преобразовании временного интервала такой
способ взвешивания практически не применяется из-за сложностей в его
технической реализации по сравнению с другими методами построения преобразователей
, начиная со старшего
разряда, наиболее широко используется при построении преобразователей частоты и
напряжения в позиционный код. При преобразовании временного интервала такой
способ взвешивания практически не применяется из-за сложностей в его
технической реализации по сравнению с другими методами построения преобразователей ![]() .
.
1.4.3.
Модели преобразователей ![]() с формированием
с формированием ![]() , начиная с младшего разряда
, начиная с младшего разряда
Для
рассматриваемых далее моделей преобразователей процесс формирования функций
включения ![]() при нахождении
при нахождении ![]() (1.18) имеет циклический характер.
Поэтому перед началом преобразования
(1.18) имеет циклический характер.
Поэтому перед началом преобразования ![]() . Нахождение
. Нахождение ![]() , начиная с младшего разряда,
базируется на известном принципе (алгоритме) преобразования целого числа
, начиная с младшего разряда,
базируется на известном принципе (алгоритме) преобразования целого числа ![]() , в том числе и унитарного, в его
двоично-позиционное представление
, в том числе и унитарного, в его
двоично-позиционное представление ![]() путем
последовательного деления
путем
последовательного деления ![]() (и получающихся
от деления частных
(и получающихся
от деления частных ![]() ) на два. Процесс деления
заканчивается, когда
) на два. Процесс деления
заканчивается, когда ![]() . С учетом начального
условия последовательность из
. С учетом начального
условия последовательность из ![]() получаемых
остатков
получаемых
остатков ![]() от деления, начиная с последнего
от деления, начиная с последнего ![]() , образует биты
, образует биты ![]() кода
кода ![]() ,
т.е.:
,
т.е.:
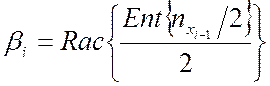 ,
,
где ![]() ;
;
![]() .
.
Применение данного приема
получения ![]() требует предварительного
преобразования
требует предварительного
преобразования ![]() аналоговой величины
аналоговой величины ![]() в целое число
в целое число ![]() , которое показывает количество
квантов (интервалов)
, которое показывает количество
квантов (интервалов) ![]() , содержащееся в
, содержащееся в ![]() , и соответственно номер интервала аппроксимации
, и соответственно номер интервала аппроксимации
![]() , которому принадлежит
, которому принадлежит ![]() .
.
Указанные выше действия можно отобразить в виде следующей последовательности операций.
1. Получение целого числа ![]() как унитарного цифрового эквивалента
как унитарного цифрового эквивалента ![]() :
:
![]() , (1.22)
, (1.22)
где ![]() ,
,
![]() – биты числа
– биты числа ![]() ;
; ![]() .
.
2. Формирование последовательности бит ![]() для двоично-взвешенного значения
для двоично-взвешенного значения ![]() на основе полученного
на основе полученного ![]() , т.е. собственно преобразование
, т.е. собственно преобразование ![]() , которое осуществляется путем
последовательного деления
, которое осуществляется путем
последовательного деления ![]() на 2, начиная с
на 2, начиная с ![]() до получения значения
до получения значения ![]() , равного нулю:
, равного нулю:
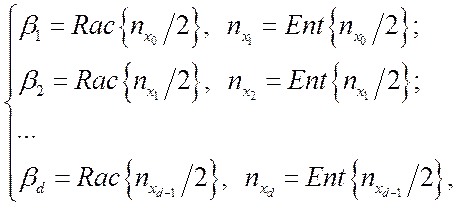 (1.23)
(1.23)
где ![]() при
при
![]() и
и ![]() при
при
![]() .
.
Совокупность действий
(1.22) и (1.23) составляет основу формирования последовательности функций
включения ![]() (
(![]() ;
;
![]() ) с учетом начала цикла
преобразования
) с учетом начала цикла
преобразования ![]() с нулевого значения
с нулевого значения ![]() .
.
Математическая и
структурная (рис. 1.14) модели преобразователя ![]() с
раздельным формированием
с
раздельным формированием ![]() и
и ![]() строятся путем реализации
зависимостей (1.22) и (1.23) на основе применения операций математического
нейрона.
строятся путем реализации
зависимостей (1.22) и (1.23) на основе применения операций математического
нейрона.
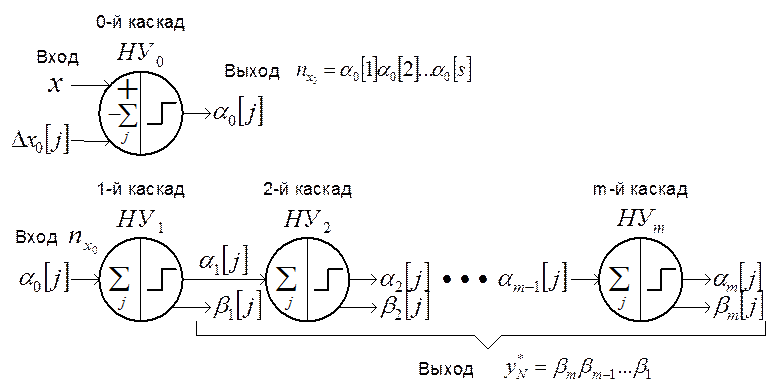
Рис. 1.14.
Нейроподобная структура Пр ![]() с раздельным
нахождением
с раздельным
нахождением ![]() и
и ![]() чисел
чисел
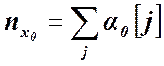 и
и ![]() ,
начиная с младшего бита
,
начиная с младшего бита ![]() (1.24) – (1.27)
(1.24) – (1.27)
Так, получение бит ![]() числа
числа ![]() в
виде число-импульсного кода
в
виде число-импульсного кода
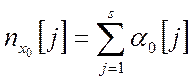 (1.24)
(1.24)
производится, по аналогии с
выражением (1.17), с помощью нейроузла ![]() последовательно
по тактам
последовательно
по тактам ![]() в соответствии с
зависимостью:
в соответствии с
зависимостью:
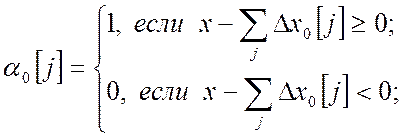 (1.25)
(1.25)
где ![]() ;
;
![]() – завершающий такт преобразования
– завершающий такт преобразования ![]() . Здесь и далее
. Здесь и далее ![]() ;
; ![]() при
при
![]() и
и ![]() =1
при
=1
при ![]() ;
; ![]() .
.
Далее последовательность ![]() (1.24) поступает на вход цепочки
нейроузлов
(1.24) поступает на вход цепочки
нейроузлов ![]() –
– ![]() ,
которые совместно выполняют совокупность операций активации при формировании
,
которые совместно выполняют совокупность операций активации при формировании ![]() и прореживания в два раза входного
потока единичных импульсов
и прореживания в два раза входного
потока единичных импульсов ![]() (т.е. деления
(т.е. деления ![]() на 2 с целью получения
на 2 с целью получения 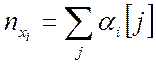 согласно (1.23)) за счет разрешения
битами
согласно (1.23)) за счет разрешения
битами ![]() передачи на выход
передачи на выход ![]() нейрона
нейрона ![]() выбранных
сигналов
выбранных
сигналов ![]() (см. рис. 1.14):
(см. рис. 1.14):
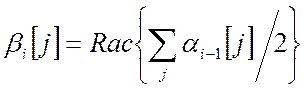 , (1.26)
, (1.26)
![]() , (1.27)
, (1.27)
где ![]() –
номера бит
–
номера бит ![]() кода
кода ![]() ;
;
![]() ;
; ![]() .
Параметр
.
Параметр ![]() указывает на интервалы
указывает на интервалы ![]() (такты) определения бит
(такты) определения бит ![]() . Здесь и далее
. Здесь и далее ![]() .
.
Рассматриваемая модель
преобразователя ![]() в виде совокупности (1.24) – (1.27)
фактически описывает известные структуры Пр
в виде совокупности (1.24) – (1.27)
фактически описывает известные структуры Пр ![]() и
и
![]() , формирующие код
, формирующие код ![]() через промежуточное преобразование
временного интервала
через промежуточное преобразование
временного интервала ![]() или частоты
или частоты ![]() в число-импульсный код
в число-импульсный код ![]() , реализуемое, в свою очередь, как
система операций математического нейрона (1.29) – (1.30). Следует
отметить, что зависимость (1.31) описывает функционирование формального нейрона
с активационной функцией
, реализуемое, в свою очередь, как
система операций математического нейрона (1.29) – (1.30). Следует
отметить, что зависимость (1.31) описывает функционирование формального нейрона
с активационной функцией ![]() с учетом
преобразований бит
с учетом
преобразований бит ![]() на предыдущих тактах (см.
рис. 1.14). Функции такого вида формируются, в частности, рекуррентной
нейронной сетью с обратными связями от выходного слоя, что предопределяет ее
применение для синтеза ИНС-преобразователей с обучаемой конструкцией.
на предыдущих тактах (см.
рис. 1.14). Функции такого вида формируются, в частности, рекуррентной
нейронной сетью с обратными связями от выходного слоя, что предопределяет ее
применение для синтеза ИНС-преобразователей с обучаемой конструкцией.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.