Для решения
задачи построения моделей ПФИ возможны различные варианты представления и
методы вычисления зависимостей (1.6) и (1.7), обеспечивающие для удобства
осуществления структурного синтеза преобразователя (Пр) декомпозицию его
нейроподобной структуры на ряд одинаковых нейроузлов, в частности двухвходовых,
реализующих однобитные преобразования. Модели Пр ![]() для
число-импульсного способа кодирования
для
число-импульсного способа кодирования ![]() (1.7)
базируются в основном на последовательном вычислении логических функций
включения
(1.7)
базируются в основном на последовательном вычислении логических функций
включения ![]() с совмещением формирования
приращений ординат
с совмещением формирования
приращений ординат ![]() и учете принадлежности
текущего значения аргумента
и учете принадлежности
текущего значения аргумента ![]() интервалу
интервалу ![]() . При этом зависимость (1.7) принимает
вид (рис. 1.8):
. При этом зависимость (1.7) принимает
вид (рис. 1.8):
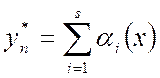 , (1.8)
, (1.8)
где ![]() .
Здесь и далее
.
Здесь и далее ![]() – номер интервала
– номер интервала ![]() , которому принадлежит значение
, которому принадлежит значение ![]() . Если
. Если ![]() ,
то в выражении (1.8)
,
то в выражении (1.8) ![]() . На интервале
. На интервале ![]() значения включений
значения включений ![]() , равные нулю, формируются либо в
соответствии с логикой их получения, либо путем начальной установки (сброса).
, равные нулю, формируются либо в
соответствии с логикой их получения, либо путем начальной установки (сброса).
При реализации
аппроксимирующей зависимости (1.7) или (1.8) нахождение для нее включений ![]() как значений пороговой бинарной функции
активации нейрона может производиться на основе следующих методов:
как значений пороговой бинарной функции
активации нейрона может производиться на основе следующих методов:
1) непосредственного (параллельного)
сравнения входной переменной ![]() с набором
значений абсцисс
с набором
значений абсцисс ![]() ;
;
2) последовательного сравнения значений
преобразуемой разности (или приращений аргумента) ![]() с
интервалом
с
интервалом ![]() ;
;
3) последовательного сравнения ![]() со значениями накапливающейся суммы
со значениями накапливающейся суммы ![]() , где
, где ![]() ;
;
![]() – величина интервала аппроксимации;
– величина интервала аппроксимации; ![]() .
.
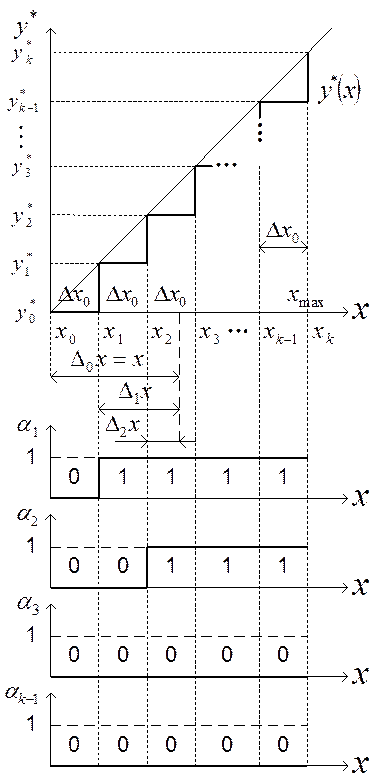
Рис. 1.8.
Зависимости ![]() и
и ![]() при
унитарном кодировании (для примера, когда
при
унитарном кодировании (для примера, когда ![]() )
)
Следует отметить, что
модели для прямого преобразования ![]() , базирующиеся на
том или ином методе получения логических функций включения (пороговых функций)
, базирующиеся на
том или ином методе получения логических функций включения (пороговых функций) ![]() , а далее также и
, а далее также и ![]() , целесообразно разделить на модели
циклического и непрерывного принципа действия. При реализации моделей
циклического типа в процедуре (процессе) преобразования четко выделяется цикл,
вызванный необходимостью проведения кодирования с некоторого начального
значения, обычно нулевого. Этот цикл завершается в определенный момент времени,
зависящий, например, от значения
, целесообразно разделить на модели
циклического и непрерывного принципа действия. При реализации моделей
циклического типа в процедуре (процессе) преобразования четко выделяется цикл,
вызванный необходимостью проведения кодирования с некоторого начального
значения, обычно нулевого. Этот цикл завершается в определенный момент времени,
зависящий, например, от значения ![]() или
или ![]() . Моделями такого рода, в частности,
описываются преобразователи
. Моделями такого рода, в частности,
описываются преобразователи ![]() , в которых
переменная
, в которых
переменная ![]() задается в виде временного интервала
задается в виде временного интервала
![]() или периода
или периода ![]() .
Их последующая техническая реализация требует включения в состав структуры
преобразователя схемы управления, обеспечивающей задание начального значения
.
Их последующая техническая реализация требует включения в состав структуры
преобразователя схемы управления, обеспечивающей задание начального значения ![]() , а также выявление окончания цикла преобразования
и фиксации результата
, а также выявление окончания цикла преобразования
и фиксации результата ![]() .
.
При построении моделей с
непрерывным характером действия такие циклы не выделяются, и кодирование ![]() производится с любого начального
состояния до получения истинного значения результата, формируемого через время,
которое затрачивается на получение всех требуемых
производится с любого начального
состояния до получения истинного значения результата, формируемого через время,
которое затрачивается на получение всех требуемых ![]() или
или
![]() . По данному принципу строится ряд
моделей преобразователей с представлением
. По данному принципу строится ряд
моделей преобразователей с представлением ![]() в
виде частоты
в
виде частоты ![]() .
.
1.3.3. Модель Пр ![]() с
формированием
с
формированием ![]() на основе
непосредственного сравнения
на основе
непосредственного сравнения ![]() с набором
значений
с набором
значений ![]()
При
непосредственном сравнении ![]() со значениями
со значениями ![]() получение
получение ![]() для
для
![]() (1.7) осуществляется параллельно для
всех
(1.7) осуществляется параллельно для
всех ![]() ‑х интервалов аппроксимации:
‑х интервалов аппроксимации:
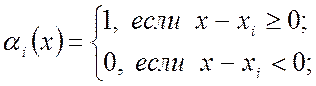 (1.9)
(1.9)
где ![]() ;
;
![]() ;
; ![]() .
.
На рис. 1.9 приведена
нейроподобная структура преобразователя ![]() ,
реализующего при вычислении (1.7) операции (1.9). Она состоит из (
,
реализующего при вычислении (1.7) операции (1.9). Она состоит из (![]() ) математических нейронов
) математических нейронов ![]() –
– ![]() ,
определяющих значения
,
определяющих значения ![]() путем реализации ими
пороговых бинарных активационных функций, и одного нейрона
путем реализации ими
пороговых бинарных активационных функций, и одного нейрона ![]() , формирующего эталонный ряд
, формирующего эталонный ряд ![]() . Для данной структуры время
преобразования
. Для данной структуры время
преобразования ![]() , затрачиваемое на
получение цифрового эквивалента
, затрачиваемое на
получение цифрового эквивалента ![]() , определяется как
максимально возможное из значений времени
, определяется как
максимально возможное из значений времени ![]() ,
, ![]() , получения функций включения
, получения функций включения ![]() :
:
![]() . (1.10)
. (1.10)
Структура, показанная на
рис. 1.9, имеет фиксированные синаптические связи. Она может быть также
получена в результате обучения однослойного персептрона. Не приводя его
конструкции и процесса обучения, необходимо отметить, что среди множества
решений по нахождению весовых коэффициентов ![]() связей
связей
![]() между нейронами распределительного
(нулевого) и обрабатывающего (одновременно выходного) слоев сети определены те,
которые приводят к формированию произведений
между нейронами распределительного
(нулевого) и обрабатывающего (одновременно выходного) слоев сети определены те,
которые приводят к формированию произведений ![]() .
.
1.3.4.
Модель Пр ![]() с получением
с получением ![]() на основе последовательного
сравнения преобразуемой разности
на основе последовательного
сравнения преобразуемой разности ![]() со значением
со значением ![]() , начиная с
, начиная с ![]()
Для метода
формирования функций включения ![]() для
для ![]() (1.7) через получение
взаимосвязанной последовательности разностей
(1.7) через получение
взаимосвязанной последовательности разностей ![]() и
их сравнения со значением
и
их сравнения со значением ![]() образование
образование ![]() , когда
, когда ![]() ,
производится, начиная с
,
производится, начиная с ![]() :
:
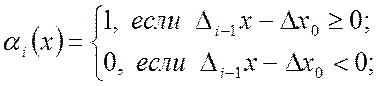 (1.11)
(1.11)
![]() , (1.12)
, (1.12)
где ![]() ;
; ![]() ;
; ![]() ;
;
![]() – номер интервала, на котором
заканчивается преобразование, т.е. когда
– номер интервала, на котором
заканчивается преобразование, т.е. когда ![]() ;
;
![]() .
.
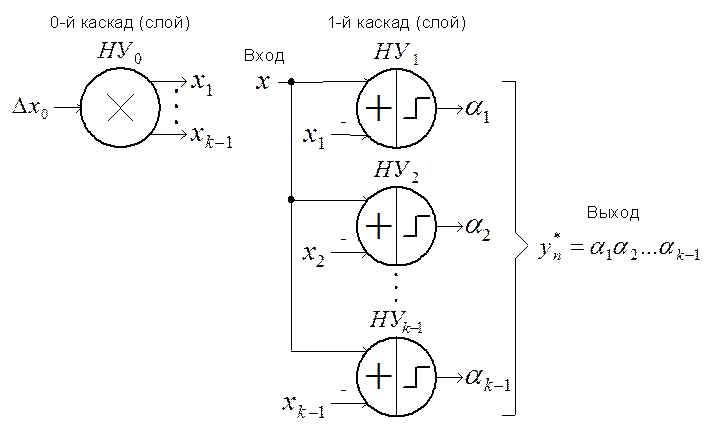
Рис. 1.9.
Структура Пр ![]() с нейросетевой
организацией на основе (1.9) или обучения сети
с нейросетевой
организацией на основе (1.9) или обучения сети
Нейроподобная структура
преобразователя ![]() (рис. 1.10,а), реализующего
(рис. 1.10,а), реализующего
![]() (1.7) через последовательное выполнение
совокупности (1.11) и (1.12), образуется путем каскадного включения (
(1.7) через последовательное выполнение
совокупности (1.11) и (1.12), образуется путем каскадного включения (![]() ) нейронов. При этом каждый ее
) нейронов. При этом каждый ее ![]() ‑й каскад состоит из одного
двухвходового нейроузла
‑й каскад состоит из одного
двухвходового нейроузла ![]() , формирующего
значения бинарной операции включения
, формирующего
значения бинарной операции включения ![]() и приращение
и приращение ![]() как сумму
как сумму ![]() на
входе его порогового элемента с функцией активации
на
входе его порогового элемента с функцией активации ![]() ,
необходимую далее для получения
,
необходимую далее для получения ![]() .
.
Для данной структуры
характерно отсутствие нейрона нулевого каскада (слоя) для формирования
эталонных значений ![]() , так как его функции реализуются
узлами
, так как его функции реализуются
узлами ![]() за счет последовательного
формирования ими приращений аргумента
за счет последовательного
формирования ими приращений аргумента ![]() ,
что значительно упрощает аппаратную реализацию Пр по сравнению со схемой,
приведенной на рис. 1.10. С этой же целью приемы каскадного включения
нейроузлов могут быть эффективно применены при построении обрабатывающих слоев
сугубо нейросетевых структур ПФИ.
,
что значительно упрощает аппаратную реализацию Пр по сравнению со схемой,
приведенной на рис. 1.10. С этой же целью приемы каскадного включения
нейроузлов могут быть эффективно применены при построении обрабатывающих слоев
сугубо нейросетевых структур ПФИ.
Разность ![]() , снимаемая с
, снимаемая с ![]() ‑го
нейроузла преобразователя (рис. 1.10,а), характеризует абсолютную погрешность
‑го
нейроузла преобразователя (рис. 1.10,а), характеризует абсолютную погрешность ![]() операции
операции ![]() .
С учетом того, что относительная погрешность преобразования
.
С учетом того, что относительная погрешность преобразования ![]() :
:
![]() , (1.13)
, (1.13)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.