Нейросетевые преобразователи импульсно-аналоговых сигналов: Учебное пособие, страница 11

Значения функций активации, формируемые нейроузлами выходного слоя, могут быть представлены (закодированы) как в виде фиксированных значений бита, равного «0» или «1», так и в виде единичного импульса . В первом случае формирование выходной величины  нейроузла  производится в соответствии с пороговой функцией активации (2.3). При использовании импульсной формы кодирования значений пороговой функции активации ее результат формируется в соответствии с выражением:

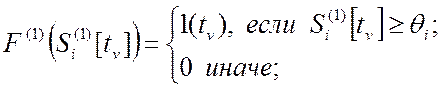                            (2.5)

где  – значение суммы на входе порогового элемента нейрона в дискретный момент времени (такт) ,  – номер такта преобразования длительностью .

С учетом количества  и  нейронов, составляющих входной и выходной слои соответственно, однослойная персептронная сеть (см. рис. 2.3), реализующая операцию преобразования , где , описывается в виде системы активационных функций:

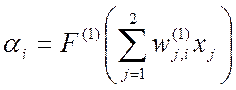,  ,                                   (2.6)

где  – входная преобразуемая аналоговая величина, представленная в виде частоты  или временного интервала ;

 – дискрет преобразования (как один из возможных эталонов), задаваемый исходя из вида преобразуемой переменной либо частотой , либо периодом  (см. табл. 1.1);

 – пороговая функция активации вида (2.3) или (2.5), для которой принимается, что операции умножения  аналоговой переменной  на цифровое значение веса  осуществляются в 1-м слое с формированием результата умножения в виде аналоговой величины.

Зависимость (2.6) в матричной форме для всех бит эквивалента  примет вид:

,                                                (2.7)

где  – матрица-строка, состоящая из входных аналоговых величин;

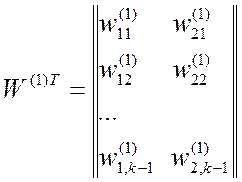 – транспонированная матрица весовых коэффициентов между распределительным и выходным слоями, в которой 1-й и 2-й столбцы соответственно содержат веса связей нейроузлов  и  со всеми  нейронами 1-го слоя;

 – матрица-столбец, состоящая из  бит эквивалента .

Необходимо отметить, что функция  в выражении (2.7) применяется над каждым элементом  матрицы . Матрица  является памятью сети, хранящей информацию о том, как должна выполняться задача преобразования информации. Цена этой памяти может быть учтена в затратах на реализацию всех синаптических связей с весами .

Таким образом, сформированная структура однослойного персептрона (см. рис. 2.3), описываемая в аналитической (2.6) и матричной (2.7) форме, является аппроксимирующей сетью, способной в результате проводимого далее обучения реализовать конкретную задачу линейного или нелинейного преобразования.

Этап 3. Обучение нейросети

На данном этапе осуществляются выбор алгоритма обучения сети на решение поставленной задачи преобразования, а затем его проведение с получением структуры и весов синаптических связей между его нейронами – как итогового результата построения нейросетевой модели ПФИ.

Обучение однослойного персептрона, как правило, осуществляется с помощью алгоритма Розенблатта или дельта-правила. Его математическая формулировка имеет вид:

,                                           (2.8)

где  – эталонное значение ‑го выхода нейронной сети;

 – номер нейрона входного слоя;

 и  – соответственно старое и новое значения весовых коэффициентов;

 – параметр, характеризующий скорость обучения, обычно , .

Кроме того, по аналогии с (2.8) могут обучаться пороговые значения  нейронов  выходного слоя:

,                                          (2.9)

,                                                       (2.10)

где  и  – соответственно старое и новое значения порога нейроузла ;  – шаг их изменения. Значение  в ряде случаев можно интерпретировать как вес  для дополнительного входа  каждого нейрона .

В качестве примера, в соответствии с (2.8) – (2.10) проведено обучение исходной аппроксимирующей сети, описанной системой (2.6), решению задачи линейного преобразования , где результат  представлен в виде (1.7). Сформированные при этом значения весов  синаптических связей сети и порогов  ее нейронов показаны на рис. 2.3. Структура этих связей отражена в виде столбцов  и  матрицы:

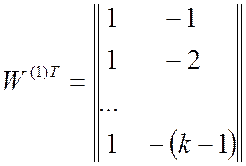.                                             (2.11)

На полученной в результате обучения структуре ИНС-преобразователя (см. рис. 2.3) над линиями его синаптических связей обозначены: слева – наименования весовых коэффициентов , а справа – их значения (например, 1) для конкретной операции преобразования. Значения порогов  для персептронных нейронов указаны над знаком порога в правом верхнем углу их изображений.

С учетом полученных коэффициентов  (2.11) и значений порогов  система (2.6), описывающая процедуру получения , примет вид:

       .                               (2.12)

Для дальнейшей физической реализации нейропреобразователя систему операций (2.12) по формированию  как бинарной активационной функции нейрона с порогом  целесообразно представить в виде:

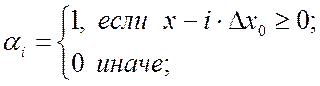
     .                     (2.13)

На основе модели (см. рис. 2.3), характеризуемой матрицей весов (2.11), целесообразно строить линейные преобразователи частоты  в унитарный позиционный код  непрерывного принципа действия, для которых входные сигналы описываются в виде матрицы , где  – дискрет преобразования. При их реализации на базе такой современной ПЛИС, как Virtex 2 фирмы Xilinx, взвешенные произведения  со значениями , заданными 2-м столбцом матрицы (2.11), могут быть сформированы с помощью ее цифрового менеджера частот (DCM). Ввиду ограниченного числа его частотных выходов такой прием получения произведений используется только при построении малоразрядных преобразователей. Если в модели преобразователя (см. рис. 2.3) вместо эталона – дискрета  принять величину , то матрица весов (2.11), полученная в результате обучения ИНС-преобразователя частоты в код, например трехразрядного, примет вид:

.

Синаптические связи с этими весами могут быть реализованы, в частности, на основе двоичного умножителя частоты.

Приведенная на рис. 2.3 сеть может быть также обучена выполнению операции нелинейного преобразования , например с монотонно убывающей первой производной (рис. 2.4).